/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2020
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 28 marca 2020 Czas pracy: 100 minut
Na rysunku przedstawiono kartkę z kalendarza na rok 2019.

Antek obchodzi urodziny 30 kwietnia, jego brat Kacper – 13 kwietnia, a siostra Beata – 3 czerwca.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W 2019 r. urodziny Kacpra wypadły w piątek. | P | F |
| W 2019 r. dniem urodzin Beaty był poniedziałek. | P | F |
Kasia zaokrągliła liczbę 21,4456 kolejno: do jedności, do części dziesiątych, do części setnych oraz części tysięcznych. Otrzymała w ten sposób cztery liczby.
O ile największa z otrzymanych liczb jest większa od najmniejszej z otrzymanych liczb? Wybierz właściwą odpowiedź spośród podanych.
A) 0,45 B) 0,446 C) 0,4 D) 0,5
W tabeli zapisano cztery wyrażenia.
| I | 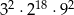 |
| II | 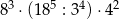 |
| III | 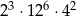 |
| IV | 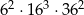 |
Które z tych wyrażeń nie jest równe 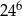 ?
?
Wybierz właściwą odpowiedź spośród podanych.
A) I B) II C) III D) IV
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 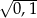 znajduje się na osi liczbowej między 0,3 i 0,4. znajduje się na osi liczbowej między 0,3 i 0,4. | P | F |
Liczba 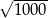 znajduje się na osi liczbowej między 31 a 32. znajduje się na osi liczbowej między 31 a 32. | P | F |
Oskar przygotował karty do gry z trzech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na sześć części, a następnie każdą z nich ponownie podzielił na sześć części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Oskar przygotował A/B kart(y) do gry.
A) 108 B) 144
Każdy gracz może otrzymać maksymalnie C/D kart(y).
C) 22 D) 21
Ośrodek pomocy społecznej przyznał zapomogę grupie kilkudziesięciu osób. Świadczenie zostało wypłacone w dwóch wysokościach: 25% osób otrzymało zapomogę w wysokości 560 zł, a pozostałe osoby otrzymały zapomogę w wyższej kwocie. Średnia arytmetyczna wypłaconych świadczeń wyniosła 605 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wyższa kwota zapomogi była równa 620 zł. | P | F |
| Gdyby niższą kwotę zapomogi obniżyć o 50 zł, a wyższą kwotę zapomogi podnieść o 50 zł, to średnia wypłaconych świadczeń nie uległaby zmianie. | P | F |
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Jeżeli 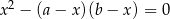 to
to
A) 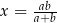 , gdy
, gdy 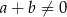 B)
B) 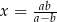 , gdy
, gdy 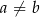
C) 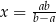 , gdy
, gdy 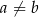 D)
D) 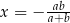 , gdy
, gdy 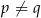
Zuzanna wybrała się na 14–kilometrową pieszą wycieczkę. Trasa wycieczki składała się z dwóch etapów, pomiędzy którymi Zuzanna zrobiła przerwę śniadaniową. Na wykresie przedstawiono jak zmieniała się w czasie odległość Zuzanny od miejsca rozpoczęcia wycieczki.
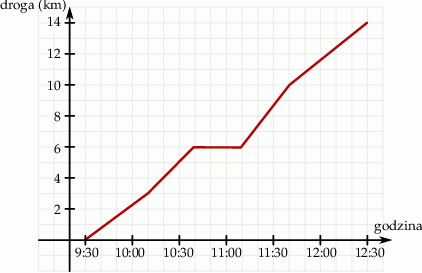
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Średnia prędkość z jaką Zuzanna pokonała drugi etap wycieczki jest równa A/B .
A) 6 km/h B) 8 km/h
Przerwa śniadaniowa zajęła C/D całego czasu poświęconego na wycieczkę.
C) 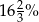 D)
D) 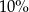
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 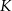 i
i 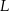 . Punkty te mają współrzędne
. Punkty te mają współrzędne 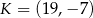 oraz
oraz 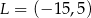 .
.
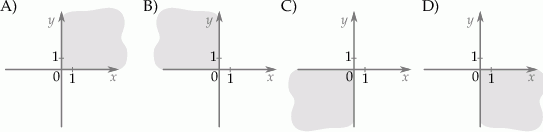
Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 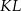 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
Bok kwadratu ma długość 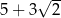 .
.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Przekątna kwadratu ma długość A/B .
A) 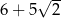 B) 11
B) 11
Pole kwadratu jest równe C/D .
C) 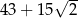 D)
D) 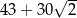
Na rysunku przedstawiono pięciokąt foremny 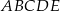
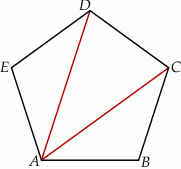
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąty 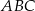 i i 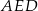 są przystające. są przystające. | P | F |
Jest 10 trójkątów o wierzchołkach w punktach 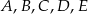 , które są przystające do trójkąta , które są przystające do trójkąta 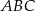 . . | P | F |
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 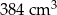 .
.
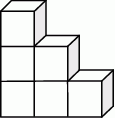
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni całkowitej tej bryły jest równe
A) 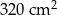 B)
B) 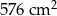 C)
C) 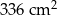 D)
D) 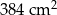
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Suma kątów wewnętrznych pięciokąta foremnego jest równa
A) 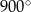 B)
B) 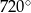 C)
C) 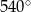 D)
D) 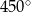
Na rysunku przedstawiono czworokąt zbudowany z dwóch trójkątów prostokątnych. Dane są długości boków 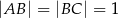 oraz
oraz 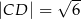 .
.
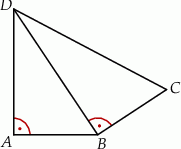
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość boku 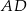 jest równa
jest równa
A) 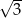 B) 2 C) 3 D)
B) 2 C) 3 D) 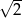
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
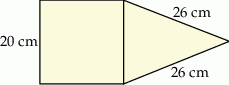
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B .
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D .
C) 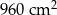 D)
D) 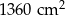
Stężenie pewnego roztworu wodnego soli wynosi 10%. Ile kilogramów czystej wody należy dodać do 12 kg tego roztworu, aby otrzymać roztwór o stężeniu 6%?
Motocykl przebył drogę 180 km w czasie 120 minut. Prędkość średnia samochodu osobowego na tej samej trasie wyniosła 72 km/h. O ile krótszy był czas przejazdu tej drogi motocyklem od czasu przejazdu samochodem osobowym?
Na boku 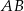 trójkąta
trójkąta 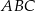 znajduje się taki punkt
znajduje się taki punkt 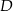 , że
, że 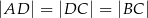 . Miara kąta
. Miara kąta 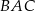 jest równa
jest równa 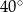 .
.
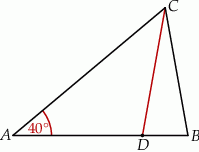
Uzasadnij, że miara kąta 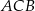 jest trzy większa od miary kąta
jest trzy większa od miary kąta 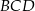 .
.
Pani Alina przez cztery tygodnie pracowała przy zbiorze owoców. W drugim tygodniu zarobiła o 20% więcej niż pierwszym, w trzecim – o 25% więcej niż w drugim, a w czwartym o 25% mniej niż w trzecim. W sumie przez cztery tygodnie Pani Alina zarobiła 2895 zł. Oblicz jakie były zarobki pani Aliny w każdym z tych czterech tygodni.
Ośmiościan foremny jest bryłą zbudowaną z ośmiu przystających trójkątów równobocznych (zobacz rysunek).
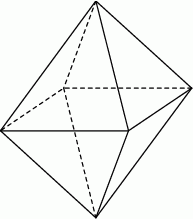
Oblicz objętość i pole powierzchni ośmiościanu foremnego, którego krawędź ma długość 6 cm.
Karol wyciął z kartonu trójkąt prostokątny 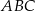 (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
(rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt 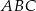 wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez 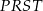 o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
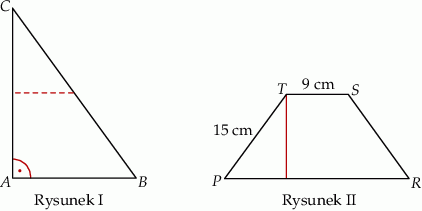
Oblicz różnicę obwodów trójkąta 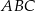 i trapezu
i trapezu 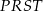 .
.

