/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2020
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 21 marca 2020 Czas pracy: 100 minut
Tomek ma do dyspozycji 6 kartoników z literami: I, V, D, L, M, X (zobacz rysunek) i układa z nich różne liczby zapisane w systemie rzymskim, przy czym za każdym razem używa wszystkich sześciu kartoników.
![]()
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Największa liczba jaką może ułożyć Tomek to 1666. | P | F |
| Najmniejsza liczba jaką może ułożyć Tomek to 1544. | P | F |
Liczba 15000 jest zaokrągleniem do rzędu dziesiątek kilku liczb naturalnych.
Ile jest wszystkich liczb naturalnych różnych od 15000, które mają takie zaokrąglenie? Wybierz właściwą odpowiedź spośród podanych.
A) 9 B) 10 C) 99 D) 100
Dane są liczby 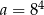 i
i 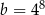 .
.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Aby otrzymać liczbę 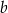 należy liczbę
należy liczbę  A/B .
A/B .
A) podnieść do kwadratu. B) pomnożyć przez 16.
Aby otrzymać liczbę 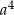 należy liczbę
należy liczbę 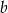 C/D .
C/D .
C) podnieść do potęgi 3. D) podnieść do potęgi 2.
Dane są cztery wyrażenia:

Wartość którego z tych wyrażeń jest najmniejsza? Wybierz właściwą odpowiedź spośród podanych.
A) I B) II C) III D) IV
Zestaw lutowniczy składa się z lutownicy, 6 końcówek lutowniczych, 5 narzędzi lutowniczych oraz 2 pincet.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W A/B zestawach lutowniczych znajduje się 1368 końcówek lutowniczych.
A) 228 B) 171
Największa liczba zestawów lutowniczych, które można skompletować z: 95 lutownic, 442 końcówek lutowniczych, 357 narzędzi lutowniczych i 147 pincet, jest równa C/D .
C) 71 D) 73
Jacek sporządził z kwasku cytrynowego i wody roztwór czyszczący. Stosunek masy kwasku cytrynowego do masy wody w tym roztworze jest równy 2 : 23.
Ile procent masy tego roztworu stanowi masa kwasku cytrynowego? Wybierz właściwą odpowiedź spośród podanych.
A) 92% B) 8,7% C) 8% D) 80% E) 4%
Na diagramie przedstawiono wysokość kieszonkowego uczniów pewnej klasy VIII.
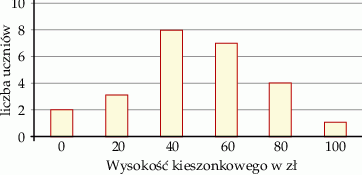
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia wysokość kieszonkowego w tej klasie jest równa 48,8 zł. | P | F |
| Każdy z ponad połowy uczniów tej klasy otrzymuje mniej niż 50 zł kieszonkowego. | P | F |
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Wyrażenie 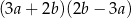 jest równe
jest równe
A) 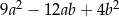 B)
B) 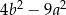 C)
C) 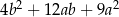 D)
D) 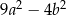
Na rysunku przedstawiono równoległobok  .
.
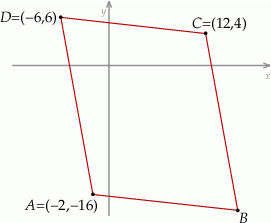
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek symetrii równoległoboku 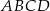 ma współrzędne ma współrzędne 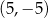 . . | P | F |
Wierzchołek  ma współrzędne ma współrzędne 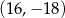 . . | P | F |
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające trójkąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
przedstawiony na rysunku I rozcięto na dwa przystające trójkąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
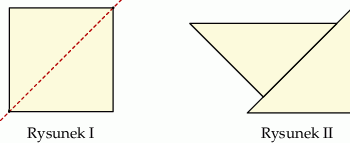
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód ułożonej figury jest większy o mniej niż  od obwodu kwadratu. od obwodu kwadratu. | P | F |
Obwód ułożonej figury jest równy 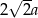 . . | P | F |
Tosia wybrała się na wycieczkę rowerową, której długość na mapie w skali 1:75 000 jest równa 22 cm. Tosia pokonała całą trasę w 90 minut.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Rzeczywista długość trasy jaką pokonała Tosia jest równa A/B .
A) 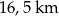 B)
B) 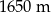
Średnia prędkość z jaką Tosia pokonała całą trasę wycieczki jest równa C/D .
C) 12 km/h D) 11 km/h
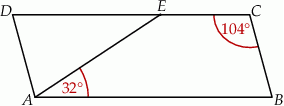
Na rysunku przedstawiono czworokąt 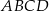 , w którym
, w którym 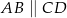 i trójkąt równoramienny
i trójkąt równoramienny 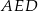 , w którym
, w którym 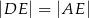 . Miara kąta
. Miara kąta 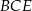 jest równa
jest równa 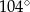 , a miara kąta
, a miara kąta 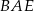 jest równa
jest równa 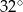 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 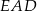 ma miarę ma miarę 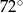 . . | P | F |
Czworokąt 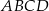 jest równoległobokiem. jest równoległobokiem. | P | F |
Odcinek 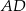 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 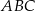 , w którym przeciwprostokątna
, w którym przeciwprostokątna 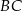 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry  ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek).
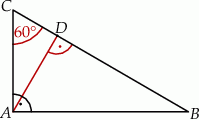
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Kąt  ma miarę A/B .
ma miarę A/B .
A) 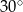 B)
B) 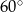
Odcinek 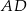 ma długość C/D .
ma długość C/D .
C) 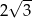 D)
D) 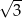
W koszu były 303 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono.
Ile klocków odłożono? Wybierz właściwą odpowiedź spośród podanych.
A) 87 B) 125 C) 178 D) 216
Na rysunku przedstawiono graniastosłup  i ostrosłup
i ostrosłup  .
.
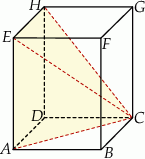
Objętość graniastosłupa jest większa od objętości ostrosłupa o 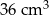 .
.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Objętość ostrosłupa 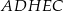 jest równa A/B .
jest równa A/B .
A) 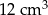 B)
B) 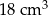
Objętość graniastosłupa 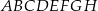 jest równa C/D .
jest równa C/D .
C) 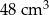 D)
D) 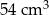
Na diagramie przedstawiono informację o wieku uczestników maratonu.
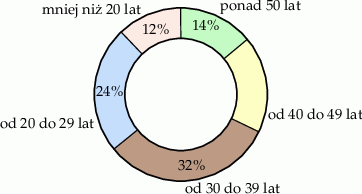
Wiadomo, że w maratonie wystartowało 288 zawodników, którzy mieli co najmniej 30 lat. Ile uczestników tego maratonu miało mniej niż 40 lat?
Wykaż, że suma trzech kolejnych liczb podzielnych przez 4 jest liczbą podzielna przez 12.
Mama Julki kupiła dwa rodzaje zeszytów – 60 kartkowe i 96 kartkowe, przy czym tych pierwszych kupiła 3 razy więcej niż tych drugich. Jeden zeszyt 60 kartkowy kosztował 3,90 zł, a jeden zeszyt 96 kartkowy kosztował 5,30 zł. Czy za wszystkie zeszyty mama Julki mogła zapłacić 102 zł?
W równoległoboku 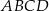 przekątna
przekątna 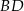 ma długość
ma długość 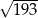 , a wysokość
, a wysokość 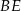 dzieli bok
dzieli bok 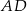 na odcinki o długościach
na odcinki o długościach 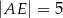 i
i 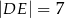 (zobacz rysunek).
(zobacz rysunek).
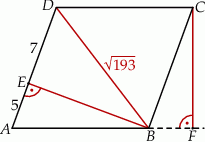
Oblicz długość wysokości 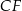 tego równoległoboku.
tego równoległoboku.
Prostokątny arkusz blachy o powierzchni 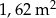 pocięto na przystające prostokąty, w sposób przedstawiony na rysunku.
pocięto na przystające prostokąty, w sposób przedstawiony na rysunku.

Jakie wymiary miał ten arkusz blachy przed pocięciem?
Trzy metalowe sześciany stopiono i z całości otrzymanego metalu odlano nowy sześcian, którego krawędź ma długość 60 cm. Dwa ze stopionych sześcianów miały krawędzie długości 30 cm i 50 cm. Jaka była długość krawędzi trzeciego ze stopionych sześcianów?

