/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 18 kwietnia 2020 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem równania 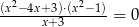 nie jest liczba
nie jest liczba
A) 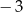 B)
B) 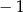 C) 1 D) 3
C) 1 D) 3
Która z poniższych liczb jest równa 3?
A) 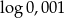 B)
B) 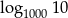 C)
C) 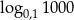 D)
D) 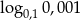
W pewnym banku oprocentowanie kredytu konsumpcyjnego przez cały marzec było równe 17%. Na początku kwietnia podwyższono oprocentowanie tego kredytu o 3 punkty procentowe, a na początku maja obniżono o 4 punkty procentowe. Oznacza to, że oprocentowanie tego kredytu konsumpcyjnego między kwietniem a majem zmalało o
A) 5% B) 3% C) 25% D) 20%
Kwadrat liczby  jest większy o co najmniej 4 od kwadratu liczby
jest większy o co najmniej 4 od kwadratu liczby  pomniejszonej o 2. Zatem
pomniejszonej o 2. Zatem
A) 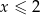 B)
B) 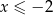 C)
C) 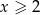 D)
D) 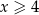
Punkty 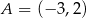 i
i 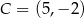 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 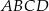 . Długość przekątnej
. Długość przekątnej 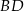 tego prostokąta jest równa
tego prostokąta jest równa
A) 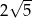 B)
B) 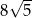 C)
C) 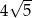 D)
D) 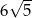
Miejscami zerowymi funkcji kwadratowej 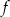 określonej wzorem
określonej wzorem 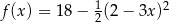 są liczby
są liczby
A) 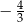 oraz
oraz 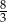 B)
B) 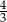 oraz
oraz 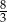 C)
C) 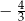 oraz
oraz 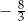 D)
D) 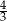 oraz
oraz 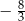
Która z liczb jest rozwiązaniem równania 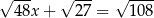 ?
?
A) 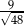 B)
B)  C)
C) 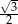 D)
D) 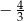
Układ równań 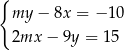 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 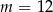 B)
B) 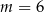 C)
C) 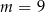 D)
D) 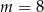
W ciągu arytmetycznym 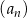 , określonym dla
, określonym dla 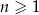 , spełniony jest warunek
, spełniony jest warunek 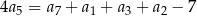 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 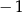 B)
B) 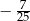 C)
C) 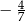 D) 2
D) 2
W ciągu 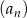 określonym dla każdej liczby
określonym dla każdej liczby 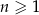 jest spełniony warunek
jest spełniony warunek 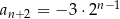 . Wtedy
. Wtedy
A) 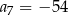 B)
B) 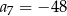 C)
C) 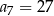 D)
D) 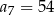
Liczbą całkowitą nie jest
A) 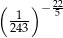 B)
B) 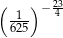 C)
C) 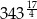 D)
D) 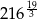
W ciągu geometrycznym 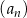 , określonym dla
, określonym dla 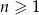 , wszystkie wyrazy są niezerowe, oraz iloczyn
, wszystkie wyrazy są niezerowe, oraz iloczyn 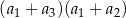 jest trzy razy mniejszy od pierwszego wyrazu tego ciągu. Suma czterech początkowych wyrazów ciągu
jest trzy razy mniejszy od pierwszego wyrazu tego ciągu. Suma czterech początkowych wyrazów ciągu 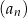 jest równa
jest równa
A) 3 B) 1 C) 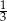 D) 9
D) 9
Dany jest trapez 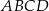 , w którym
, w którym 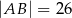 ,
, 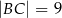 ,
, 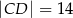 i
i 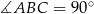 (zobacz rysunek).
(zobacz rysunek).
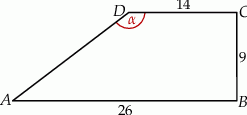
Stąd wynika, że cosinus zaznaczonego na rysunku kąta  jet równy
jet równy
A)  B)
B) 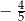 C)
C) 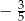 D)
D) 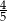
Dany jest trójkąt równoramienny 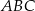 , w którym
, w którym 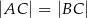 . Na podstawie
. Na podstawie 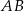 tego trójkąta leży punkt
tego trójkąta leży punkt 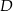 , taki że
, taki że 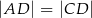 ,
, 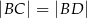 oraz
oraz 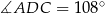 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że kąt  ma miarę
ma miarę
A)  B)
B) 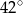 C)
C) 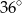 D)
D) 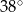
Okrąg, którego środkiem jest punkt 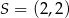 , jest styczny do prostej
, jest styczny do prostej 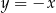 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 2 B) 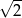 C)
C) 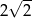 D) 4
D) 4
Na okręgu o środku w punkcie 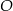 wybrano trzy punkty
wybrano trzy punkty 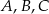 tak, że
tak, że  ,
,  . Cięciwa
. Cięciwa  przecina promień
przecina promień 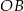 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 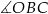 jest równa
jest równa
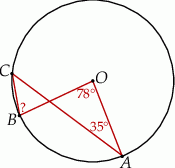
A) 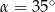 B)
B) 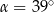 C)
C) 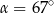 D)
D) 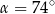
Prosta o równaniu 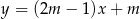 nie przecina prostej o równaniu
nie przecina prostej o równaniu 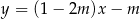 . Zatem
. Zatem
A) 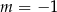 B)
B) 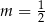 C)
C) 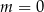 D)
D) 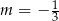
W układzie współrzędnych dany jest trójkąt o wierzchołkach 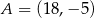 ,
, 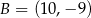 i
i 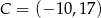 . Na boku
. Na boku 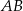 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 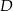 tak, że pole trójkąta
tak, że pole trójkąta 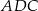 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 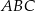 . Wówczas
. Wówczas
A) 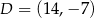 B)
B) 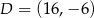 C)
C) 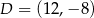 D)
D) 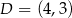
W układzie współrzędnych na płaszczyźnie dany jest punkt 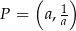 , gdzie
, gdzie  jest pewną liczbą niezerową. Punkt
jest pewną liczbą niezerową. Punkt 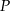 może należeć do tej samej ćwiartki układu współrzędnych, co punkt
może należeć do tej samej ćwiartki układu współrzędnych, co punkt
A) 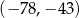 B)
B)  C)
C) 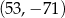 D)
D) 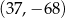
Na diagramie przedstawiono procentowy podział zarobków w pewnej firmie
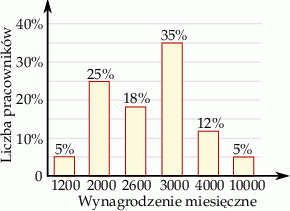
Jaki procent pracowników tej firmy ma zarobki powyżej średniej?
A) 47% B) 52% C) 5% D) 17%
Ze zbioru cyfr 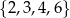 losujemy kolejno ze zwracaniem trzy cyfry i zapisujemy je, tworząc liczbę trzycyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
losujemy kolejno ze zwracaniem trzy cyfry i zapisujemy je, tworząc liczbę trzycyfrową. Ile jest możliwości utworzenia w ten sposób liczby podzielnej przez 3?
A) 10 B) 16 C) 22 D) 24
Ceramiczna ozdoba ma kształt czworościanu foremnego o krawędzi długości 6 dm (zobacz rysunek).
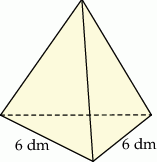
Wysokość tego czworościanu jest – z dokładnością do 0,01 dm – równa
A) 3,46 dm B) 4,9 dm C) 5,2 dm D) 4,8 dm
Graniastosłup prosty ma pole powierzchni całkowitej równe 94, a w jego podstawie jest prostokąt o bokach długości 3 i 4 (zobacz rysunek).
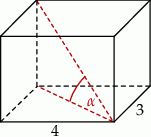
Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
A) 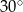 B)
B) 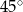 C)
C) 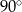 D)
D) 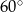
Przekrojem osiowym walca jest kwadrat o przekątnej długości 16. Objętość tego walca jest zatem równa
A) 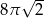 B)
B) 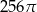 C)
C) 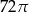 D)
D) 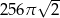
W pudełku jest 60 kul. Wśród nich jest 27 kul białych, 18 kul niebieskich, a pozostałe to kule żółte. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę, która nie jest niebieska, jest równe
A) 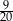 B)
B) 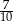 C)
C) 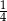 D)
D) 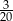
Zadania otwarte
Funkcja kwadratowa 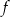 jest określona wzorem
jest określona wzorem 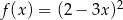 . Wyznacz wszystkie argumenty
. Wyznacz wszystkie argumenty  , dla których:
, dla których: 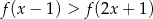 .
.
Wyznacz wszystkie liczby rzeczywiste  , które spełniają warunek:
, które spełniają warunek: 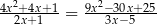 .
.
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 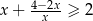 .
.
W ciągu geometrycznym przez 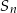 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 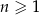 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 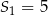 i
i 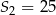 . Wyznacz iloraz i szósty wyraz tego ciągu.
. Wyznacz iloraz i szósty wyraz tego ciągu.
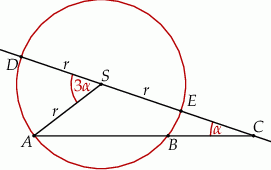
Dany jest okrąg o środku w punkcie 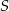 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 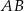 poza punkt
poza punkt 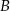 odłożono odcinek
odłożono odcinek 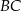 . Przez punkty
. Przez punkty 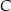 i
i 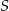 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 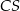 przecina dany okrąg w punktach
przecina dany okrąg w punktach 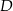 i
i 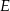 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 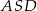 jest trzy razy większa od miary kąta
jest trzy razy większa od miary kąta 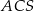 , to
, to 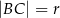 .
.
Dany jest ostrosłup o podstawie pięciokątnej 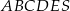 (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 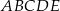 . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
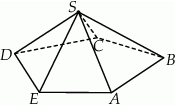
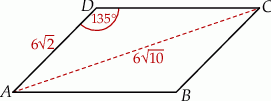
Dany jest równoległobok 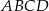 , w którym kąt rozwarty
, w którym kąt rozwarty 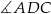 ma miarę
ma miarę 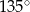 . Ponadto wiadomo, że
. Ponadto wiadomo, że 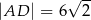 i
i 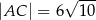 (zobacz rysunek). Oblicz obwód tego równoległoboku.
(zobacz rysunek). Oblicz obwód tego równoległoboku.
Dany jest punkt 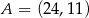 . Prosta o równaniu
. Prosta o równaniu 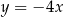 jest symetralną odcinka
jest symetralną odcinka 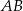 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 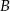 .
.
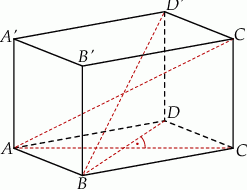
Podstawą graniastosłupa prostego 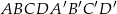 jest romb
jest romb 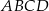 . Przekątna
. Przekątna 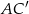 tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 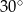 , a przekątna
, a przekątna 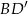 ma długość
ma długość 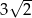 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.