/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 4 kwietnia 2020 Czas pracy: 180 minut
Zadania zamknięte
Jeżeli 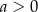 , to liczba
, to liczba 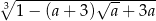 jest równa
jest równa
A) 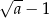 B)
B) 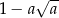 C)
C) 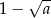 D)
D) 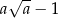
W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
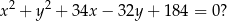
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
Liczba 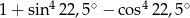 jest równa
jest równa
A) 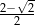 B) 1 C)
B) 1 C) 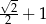 D) 2
D) 2
Zdarzenia losowe 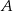 i
i 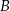 zawarte w
zawarte w 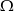 są takie, że prawdopodobieństwo
są takie, że prawdopodobieństwo 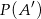 zdarzenia
zdarzenia 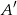 , przeciwnego do zdarzenia
, przeciwnego do zdarzenia 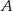 , jest równe
, jest równe  . Ponadto, prawdopodobieństwo warunkowe
. Ponadto, prawdopodobieństwo warunkowe 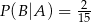 . Wynika stąd, że
. Wynika stąd, że
A) 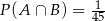 B)
B) 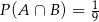 C)
C) 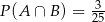 D)
D) 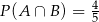
Liczba rzeczywistych rozwiązań równania 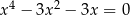 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Zadania otwarte
W trójkącie 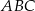 punkt
punkt 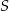 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 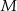 i
i 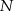 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 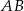 i
i 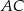 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 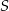 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 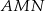 .
.
Uzasadnij, że dla dowolnych liczb dodatnich  i
i 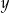 prawdziwa jest nierówność
prawdziwa jest nierówność
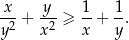
Wyznacz te wartości parametru 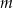 , dla których równanie
, dla których równanie 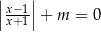 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Wyznacz wszystkie wartości parametru  , dla których prosta o równaniu
, dla których prosta o równaniu 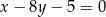 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 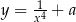 .
.
Oblicz, ile jest ośmiocyfrowych liczb naturalnych takich, że iloczyn wszystkich ich cyfr w zapisie dziesiętnym jest równy 1323.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
Rozwiąż równanie 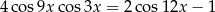 w przedziale
w przedziale 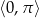 .
.
Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.
Przekątna 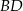 deltoidu zawiera się w prostej o równaniu
deltoidu zawiera się w prostej o równaniu 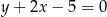 i ma taką samą długość jak przekątna
i ma taką samą długość jak przekątna 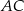 . Przekątne te przecinają się w punkcie
. Przekątne te przecinają się w punkcie 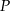 , takim że
, takim że 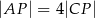 . Wierzchołek
. Wierzchołek 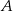 ma współrzędne
ma współrzędne 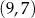 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 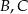 i
i 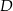 tego deltoidu.
tego deltoidu.
Trzywyrazowy ciąg 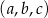 o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
o wyrazach dodatnich jest arytmetyczny, natomiast ciąg
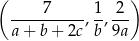
jest geometryczny. Oblicz iloraz ciągu geometrycznego.
Zakład produkcyjny planuje wytwarzanie pojemników o objętości 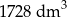 , które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).
, które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).
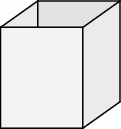
Koszt produkcji 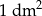 podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji
podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji 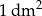 jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.
jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.

