/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 21 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Iloczyn wszystkich rzeczywistych pierwiastków równania
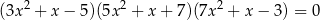
jest równy
A) 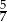 B) 1 C)
B) 1 C) 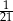 D)
D) 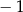
Liczba 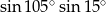 jest równa
jest równa
A) 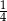 B)
B) 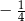 C)
C) 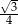 D)
D) 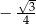
Liczba punktów wspólnych wykresów funkcji 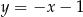 i
i 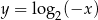 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Nieskończony ciąg geometryczny 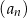 spełnia warunki:
spełnia warunki: 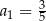 oraz
oraz 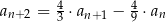 dla
dla 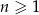 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 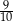 B)
B) 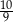 C)
C)  D)
D) 
Kasia wykonała rzut trzema sześciennymi kostkami do gry i otrzymała sumę oczek większą niż 16. Prawdopodobieństwo, że Kasia wyrzuciła trzy szóstki jest równe
A) 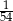 B)
B)  C)
C) 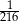 D)
D) 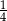
Zadania otwarte
Wyznacz maksymalne przedziały monotoniczności funkcji 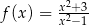 .
.
Liczby naturalne 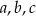 są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba
są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba  spełnia warunek
spełnia warunek
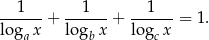
Wykaż, że  jest sześcianem liczby naturalnej.
jest sześcianem liczby naturalnej.
Na okręgu o środku 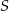 wybrano punkty
wybrano punkty 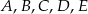 w ten sposób, że odcinek
w ten sposób, że odcinek 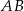 jest średnicą okręgu oraz
jest średnicą okręgu oraz 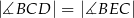 (zobacz rysunek).
(zobacz rysunek).
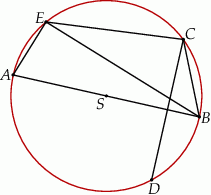
Wykaż, że proste 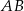 i
i 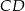 są prostopadłe.
są prostopadłe.
Oblicz granicę 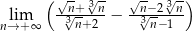 .
.
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 4, 5, 6, 7, 8 bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
Okrąg  ma środek
ma środek 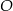 i jest styczny prostej
i jest styczny prostej 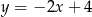 w punkcie
w punkcie 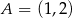 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu  , jeżeli
, jeżeli ![−→ OA = [2,1]](https://img.zadania.info/zes/0068148/HzesT41x.gif) .
.
Funkcja 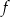 określona jest wzorem
określona jest wzorem 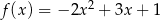 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 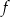 , które przechodzą przez punkt
, które przechodzą przez punkt 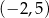 .
.
Rozwiąż równanie ![(sin x)⋅[co s(x − π-)+ cos(x + π)] = 3co sx 6 6 2](https://img.zadania.info/zes/0068148/HzesT47x.gif) .
.
Punkt 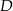 leży na boku
leży na boku 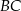 trójkąta
trójkąta 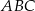 oraz
oraz 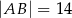 ,
, 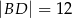 ,
, 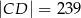 i
i 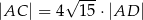 . Oblicz pole trójkąta
. Oblicz pole trójkąta 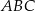 .
.
Podstawą ostrosłupa jest trójkąt o danych kątach  i
i 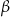 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 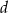 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze 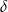 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wyznacz wszystkie wartości parametru 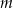 , dla których równanie
, dla których równanie
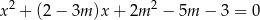
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 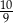 .
.
Rozpatrujemy wszystkie czworokąty 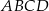 , które są jednoczenie wpisane w okrąg i opisane na okręgu, w których
, które są jednoczenie wpisane w okrąg i opisane na okręgu, w których 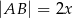 ,
, 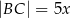 , i których obwód jest równy 10.
, i których obwód jest równy 10.
Pole czworokąta 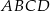 wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
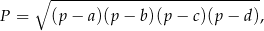
gdzie 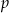 – jest połową obwodu czworokąta.
– jest połową obwodu czworokąta.
Zapisz pole czworokąta 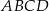 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.

