/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 21 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Liczba 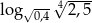 jest równa
jest równa
A) 2 B) 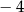 C)
C) 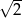 D)
D) 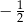
Jeżeli 59% liczby 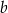 jest równe 177 i
jest równe 177 i 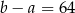 , to 75% liczby
, to 75% liczby  jest równe
jest równe
A) 236 B) 300 C) 225 D) 177
Jedną z liczb spełniających nierówność 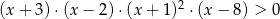 jest
jest
A) 3 B) 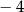 C)
C) 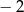 D) 7
D) 7
Liczba 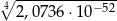 jest równa
jest równa
A) 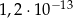 B)
B) 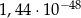 C)
C) 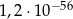 D)
D) 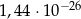
Para liczb 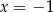 i
i 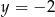 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 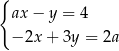 dla
dla
A) 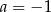 B)
B) 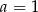 C)
C) 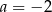 D)
D) 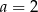
Równanie 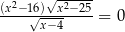 ma dokładnie
ma dokładnie
A) cztery rozwiązania B) trzy rozwiązania
C) dwa rozwiązania D) jedno rozwiązanie
Jeśli wykres funkcji kwadratowej 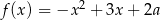 jest styczny do prostej
jest styczny do prostej 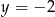 , to
, to
A) 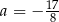 B)
B) 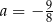 C)
C) 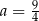 D)
D) 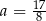
Rysunek przedstawia wykres funkcji 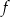 określonej dla
określonej dla 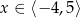 .
.
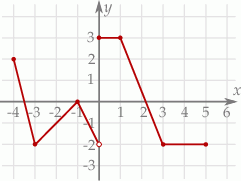
Równanie 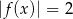 ma
ma
A) dokładnie dwa rozwiązania. B) dokładnie cztery rozwiązania.
C) dokładnie pięć rozwiązań. D) nieskończenie wiele rozwiązań.
Dany jest ciąg geometryczny 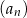 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 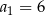 . Jeżeli
. Jeżeli 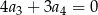 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 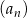 jest
jest
A) 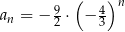 B)
B) 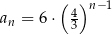 C)
C) 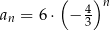 D)
D) 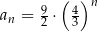
Punkt 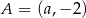 leży na prostej określonej równaniem
leży na prostej określonej równaniem 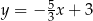 . Stąd wynika, że
. Stąd wynika, że
A) 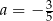 B)
B) 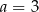 C)
C) 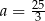 D)
D) 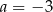
W ciągu arytmetycznym 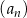 dane są
dane są 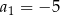 ,
, 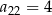 i
i 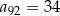 . Wtedy suma
. Wtedy suma
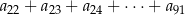
jest równa
A) 1293 B) 1315 C) 1311 D) 1345
Kąt 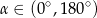 spełnia warunek:
spełnia warunek: 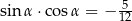 . Wartość wyrażenia
. Wartość wyrażenia 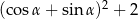 jest równa
jest równa
A) 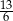 B)
B) 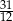 C)
C) 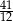 D)
D) 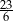
Wyrażenie 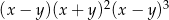 jest równe
jest równe
A) 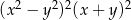 B)
B) 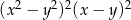
C) 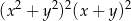 D)
D) 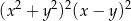
Wskaż nierówność, którą spełnia liczba 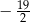 .
.
A) 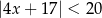 B)
B) 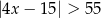 C)
C) 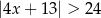 D)
D) 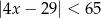
Dane są dwa okręgi: okrąg o środku w punkcie 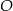 i promieniu 4 oraz okrąg o środku w punkcie
i promieniu 4 oraz okrąg o środku w punkcie 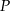 i promieniu 6. Odcinek
i promieniu 6. Odcinek 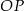 ma długość 25. Prosta
ma długość 25. Prosta 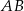 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 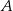 i
i 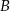 . Ponadto prosta
. Ponadto prosta 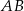 przecina odcinek
przecina odcinek 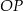 w punkcie
w punkcie 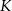 (zobacz rysunek).
(zobacz rysunek).
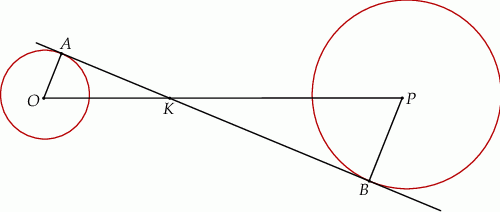
Wtedy
A) 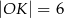 B)
B) 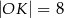 C)
C) 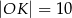 D)
D) 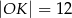
Ze zbioru liczb całkowitych, które są zawarte w przedziale 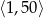 losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
A) 0,0048 B) 0,0028 C) 0,0024 D) 0,0052
Liczba dzielników naturalnych liczby 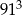 jest równa
jest równa
A) 8 B) 256 C) 16 D) 4
Odcinek 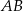 jest średnicą okręgu o środku
jest średnicą okręgu o środku 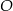 (rysunek).
(rysunek).
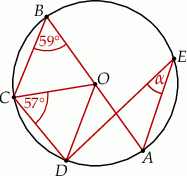
Miara kąta  jest równa
jest równa
A) 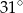 B)
B) 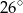 C)
C) 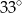 D)
D) 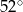
Podstawą ostrosłupa jest kwadrat  o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 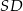 , a długość krawędzi
, a długość krawędzi 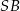 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
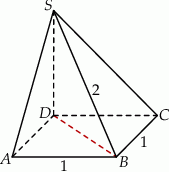
Różnica miar kątów 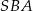 i
i 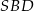 jest równa
jest równa
A) 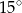 B)
B) 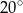 C)
C) 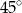 D)
D) 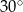
Punkt 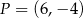 , przekształcono w symetrii względem prostej
, przekształcono w symetrii względem prostej 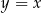 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 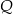 . Zatem
. Zatem
A) 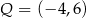 B)
B) 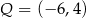 C)
C) 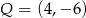 D)
D) 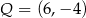
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 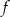 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 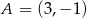 i
i 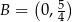 .
.
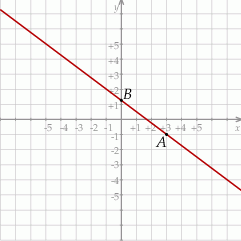
Obrazem prostej 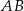 przy obrocie o kąt
przy obrocie o kąt 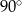 wokół punktu
wokół punktu 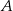 jest wykres funkcji
jest wykres funkcji 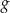 określonej wzorem
określonej wzorem
A) 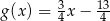 B)
B) 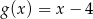 C)
C) 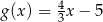 D)
D) 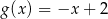
Suma długości wszystkich krawędzi sześcianu jest równa 108 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 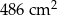 B)
B) 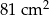 C)
C) 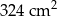 D)
D) 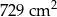
Okrąg o środku 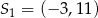 oraz okrąg o środku
oraz okrąg o środku 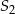 i promieniu 6 są styczne wewnętrznie w punkcie
i promieniu 6 są styczne wewnętrznie w punkcie 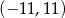 . Wtedy
. Wtedy
A) 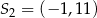 B)
B) 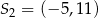 C)
C) 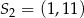 D)
D) 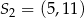
Punkty 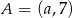 ,
, 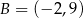 i
i 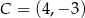 są wierzchołkami trójkąta równoramiennego o podstawie
są wierzchołkami trójkąta równoramiennego o podstawie 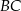 . Zatem
. Zatem
A) 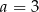 B)
B) 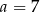 C)
C) 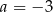 D)
D) 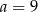
Mediana zestawu ośmiu danych liczb: 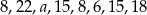 jest równa 14. Zatem
jest równa 14. Zatem
A) 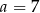 B)
B) 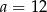 C)
C) 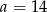 D)
D) 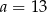
Zadania otwarte
Rozwiąż równanie 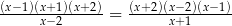 .
.
Rozwiąż nierówność 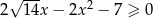 .
.
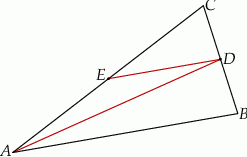
Punkty  i
i  są środkami boków
są środkami boków 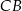 i
i 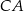 trójkąta
trójkąta 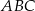 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 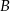 od prostej
od prostej 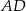 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 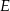 od prostej
od prostej 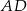 .
.
Uzasadnij, że jeżeli liczby rzeczywiste 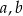 spełniają warunek
spełniają warunek 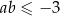 , to
, to 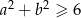 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 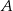 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
W trapezie prostokątnym 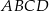 dłuższa podstawa
dłuższa podstawa 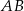 ma długość 15. Przekątna
ma długość 15. Przekątna 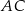 tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze 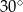 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 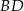 tego trapezu.
tego trapezu.
W ciągu arytmetycznym 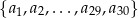 suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
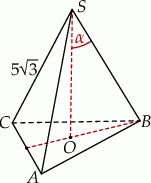
Długość krawędzi bocznej ostrosłupa prawidłowego trójkątnego  jest równa
jest równa 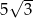 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
(zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 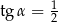 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Prosta  tworzy z dodatnią półosią
tworzy z dodatnią półosią 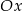 kąt o mierze
kąt o mierze 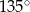 i przechodzi przez punkt
i przechodzi przez punkt 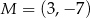 . Prosta
. Prosta 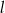 jest prostopadła do prostej
jest prostopadła do prostej 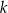 i przecina oś
i przecina oś 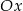 w punkcie o odciętej
w punkcie o odciętej 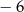 . Oblicz obwód trójkąta utworzonego przez proste
. Oblicz obwód trójkąta utworzonego przez proste 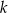 ,
,  i oś
i oś  .
.

