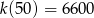/Szkoła średnia/Zadania z treścią

Zadanie nr 1012141

Dodaj do ulubionych
Dodaj do rozwiązanych

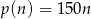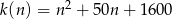W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór p (n) = 150n , gdzie n oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność k(n) = n2 + 50n + 1600 .

  • Napisz wzór funkcji 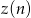z(n) - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
  • Przy jakiej wielkości produkcji zysk wynosi 0?
  • Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?

Rozwiązanie

  • Musimy od przychodu odjąć koszty produkcji.
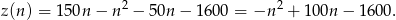
    z(n) = 150n − n2 − 50n − 160 0 = −n 2 + 100n − 1 600.

     
    Odpowiedź: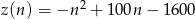 z(n) = −n 2 + 100n − 1600

  • Rozwiązujemy równanie.
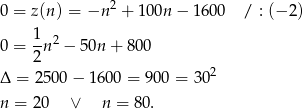
    0 = z(n) = −n 2 + 100n − 160 0 / : (− 2) 1- 2 0 = 2 n − 50n + 800 Δ = 2500 − 1600 = 900 = 30 2 n = 20 ∨ n = 80.

     
    Odpowiedź: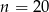 n = 2 0 lub n = 80

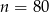
  • Wykresem funkcji zysku jest parabola o ramionach skierowanych w dół, więc największą wartość przyjmuje on w wierzchołku paraboli, czyli dla 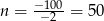−100- n = −2 = 50 . Koszt produkcji jest wtedy równy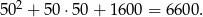
    2 50 + 50⋅ 50+ 1600 = 6 600.

     
    Odpowiedź: Dla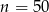 n = 50 , koszt produkcji: k(50) = 66 00

Wersja PDF