/Szkoła średnia/Zadania z treścią

Zadanie nr 1285481

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz cztery kolejne liczby całkowite takie, że sześcian największej z nich jest równy sumie sześcianów trzech pozostałych liczb.

Rozwiązanie

Oznaczmy szukane przez 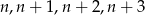n,n + 1,n + 2 ,n+ 3 . Musimy zatem wyznaczyć całkowite rozwiązania równania

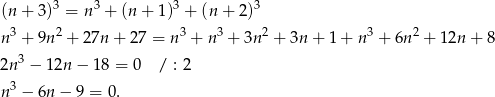
3 3 3 3 (n + 3) = n + (n+ 1) + (n+ 2) n3 + 9n 2 + 2 7n + 27 = n 3 + n 3 + 3n 2 + 3n + 1 + n3 + 6n2 + 12n + 8 2n 3 − 1 2n− 18 = 0 / : 2 3 n − 6n − 9 = 0.

Próbujemy odgadnąć jeden z pierwiastków tego równania – sprawdzamy dzielniki wyrazu wolnego. Gdy to zrobimy okaże się, że jednym z pierwiastków jest 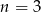n = 3 . Dzielimy więc lewą stronę równania przez 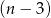(n− 3) – my zrobimy to grupując wyrazy.

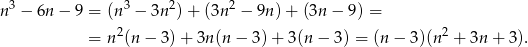
3 3 2 2 n − 6n − 9 = (n − 3n )+ (3n − 9n) + (3n − 9 ) = = n 2(n − 3)+ 3n(n − 3 )+ 3(n − 3) = (n − 3)(n2 + 3n + 3 ).

Trójmian w nawiasie nie ma pierwiastków (bo 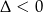Δ < 0 ), więc jedynym pierwiastkiem równania jest 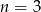n = 3 , czyli szukane liczby to 3, 4, 5, 6.  
Odpowiedź: 3, 4, 5, 6

Wersja PDF