/Szkoła średnia/Zadania z treścią

Zadanie nr 1545189

Dodaj do ulubionych
Dodaj do rozwiązanych

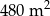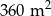Dwie prostokątne działki ogrodnicze mają odpowiednio pola powierzchni 48 0 m 2 i 360 m 2 . Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.

Rozwiązanie

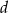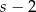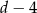Oznaczmy szerokość i długość pierwszej działki przez s i d . W takim razie druga działka ma wymiary s− 2 i d − 4 i otrzymujemy układ równań

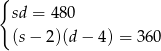
{ sd = 480 (s− 2)(d − 4 ) = 360

Przekształćmy drugie równanie korzystając z równości 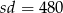sd = 480 .

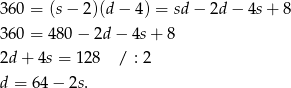
360 = (s− 2 )(d − 4 ) = sd− 2d − 4s+ 8 360 = 480 − 2d − 4s + 8 2d + 4s = 1 28 / : 2 d = 6 4− 2s.

Podstawiamy teraz tę wartość do równości 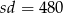sd = 480 .

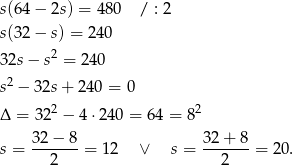
s(64 − 2s) = 480 / : 2 s(32 − s) = 240 32s − s2 = 240 2 s − 32s+ 240 = 0 Δ = 322 − 4⋅2 40 = 64 = 8 2 s = 32-−-8-= 12 ∨ s = 32+--8-= 20 . 2 2

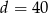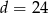Wtedy d = 40 i d = 24 odpowiednio. Zatem działki mają wymiary 12 m na 40 m i 10 m na 36 m, lub 20 m na 24 m i 18 m na 20 m.  
Odpowiedź: 12 m na 40 m i 10 m na 36 m, lub 20 m na 24 m i 18 m na 20 m

Wersja PDF