/Szkoła średnia/Zadania z treścią

Zadanie nr 1552060

Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, których ostatnia cyfra jest równa 7.

Wersja PDF

Rozwiązanie

Jeżeli zaczniemy wypisywać te liczby

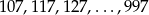
107,117,1 27,...,997

to widać, że mamy do czynienia z ciągiem arytmetycznym o pierwszym wyrazie 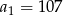a1 = 107 i różnicy 10. Aby obliczyć żądaną sumę musimy wiedzieć ile ten ciąg ma wyrazów.

Sposób I

Jeżeli wypiszemy te liczby w postaci

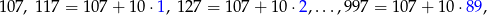
107, 117 = 107 + 1 0⋅1, 127 = 107+ 10 ⋅2,...,997 = 10 7+ 10⋅8 9,

to widać, że tych liczb jest 90. Zatem interesująca nas suma jest równa

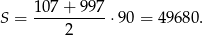
107-+-997- S = 2 ⋅90 = 49680.

Sposób II

Możemy też skorzystać ze wzoru na n -ty wyraz ciągu arytmetycznego. Rozwiązujemy równanie

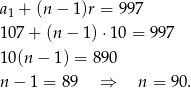
a + (n− 1)r = 997 1 107 + (n − 1) ⋅10 = 9 97 10(n − 1) = 890 n − 1 = 89 ⇒ n = 90 .

Sumę liczymy jak poprzednio.  
Odpowiedź: 49680

Wersja PDF