Zadanie nr 1606578
Uzasadnij, że suma dwóch liczb dwucyfrowych takich, że cyfra dziesiątek i cyfra jedności pierwszej z nich jest odpowiednio cyfrą jedności i cyfrą dziesiątek drugiej jest podzielna przez 11.
Rozwiązanie
Jeżeli pierwsza z liczba ma kolejno cyfry 
i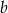 
, to jest równa 
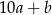. Wtedy druga liczba to 
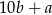i suma tych dwóch liczb to
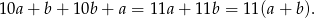
Widać teraz, że liczba ta jest podzielna przez 11.
