/Szkoła średnia/Zadania z treścią

Zadanie nr 1693446

Dodaj do ulubionych
Dodaj do rozwiązanych

Fabryka odzieży w pierwszym roku produkcji wyprodukowała 2000 kurtek i 1000 par spodni. W każdym kolejnym roku produkcję par spodni zwiększano o 400 sztuk, a produkcję kurtek zmniejszano o 20%. Po ilu latach produkcji łączna liczba (od początku działalności fabryki) wyprodukowanych par spodni przekroczy łączną liczbę wyprodukowanych kurtek?

Rozwiązanie

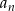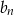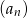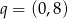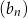Jeżeli oznaczymy liczbę wyprodukowanych kurtek w n -tym roku przez an , a liczbę wyprodukowanych par spodni przez bn to (an) jest ciągiem geometrycznym o ilorazie q = (0 ,8) , a (bn) jest ciągiem arytmetycznym o różnicy 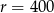r = 400 . Ze wzorów sumę początkowych wyrazów takich ciągów, wiemy, że po n -latach działalności fabryki wyprodukowano odpowiednio

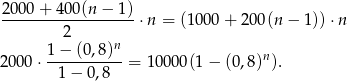
2 000+ 400(n − 1) -------------------⋅n = (1000 + 200 (n− 1))⋅n 2 1−--(0,8)n- n 200 0⋅ 1 − 0,8 = 10 000(1 − (0,8) ).

par spodni i kurtek.

Sposób I

Niespecjalnie widać w jaki sposób porównać te wyrażenia, więc spróbujmy policzyć ich wartości dla kolejnych liczb n .

n = 1 : 1 000, 2000 n = 2 : 2 400, 3600 n = 3 : 4 200, 4880 n = 4 : 6 400, 5904.

Zatem interesująca nas sytuacja nastąpi po 4 latach.  
Odpowiedź: Po 4 latach.

Wersja PDF