Zadanie nr 1708639
W pewnym nadleśnictwie postanowiono wymienić drzewostan na obszarze 150 hektarów. W pierwszym roku zaplanowano wymianę na obszarze 3 hektarów i ustalono normę, według której w każdym następnym roku będzie się dokonywać wymiany na obszarze o 1 hektar większym niż w roku poprzednim.
- Oblicz, ile lat będzie trwać wymiana drzewostanu na zaplanowanym obszarze.
- Oblicz, o ile należałoby zwiększyć normę wymiany drzewostanu, aby skrócić cały proces o 5 lat.
- W obu przypadkach oblicz liczbę hektarów, na których dokonana zostanie wymiana w ostatnim roku.
Rozwiązanie
Jeżeli przez 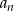 oznaczymy liczbę wyciętych hektarów lasu w
oznaczymy liczbę wyciętych hektarów lasu w  –tym roku, to mamy
–tym roku, to mamy 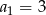 i
i 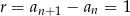 .
.
- Musimy rozwiązać równanie
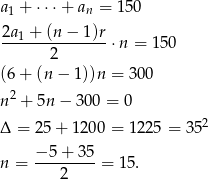
Odpowiedź: 15 lat - Niech
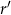 będzie normą zmiany, która pozwoli skrócić proces wymiany o 5 lat. Mamy zatem
będzie normą zmiany, która pozwoli skrócić proces wymiany o 5 lat. Mamy zatem 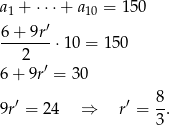
Norma musi więc większa o
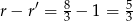 hektara.
hektara.
Odpowiedź: Należy zwiększyć o hektara
hektara - Mamy
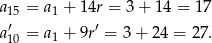
Odpowiedź: 17 i 27 hektarów

