/Szkoła średnia/Zadania z treścią

Zadanie nr 1772476

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozłożono 100 cukierków na 5 talerzach.
Na 1 i 2 talerzu znalazły się łącznie 52 cukierki,
na 2 i 3 talerzu 43 cukierki,
na 3 i 4 talerzu 34 cukierki,
na 4 i 5 talerzu 30 cukierków.
Ile cukierków znajdowało się na każdym talerzu?

Rozwiązanie

Mamy układ równań

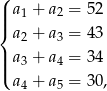
( ||| a1 + a2 = 5 2 { a2 + a3 = 4 3 | ||( a3 + a4 = 3 4 a4 + a5 = 3 0,

gdzie przez 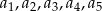a1,a2,a3,a4,a5 oznaczyliśmy liczby cukierków na kolejnych talerzach.

Sposób I

Korzystając z powyższych informacji wyliczmy ilość cukierków na każdym z talerzy w zależności od 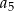a 5 .

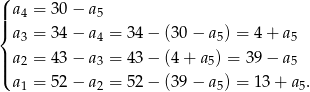
( | a4 = 30 − a5 ||{ a3 = 34 − a4 = 34 − (30 − a5) = 4+ a 5 || a2 = 43 − a3 = 43 − (4 + a5) = 3 9− a 5 |( a1 = 52 − a2 = 52 − (39 − a5) = 13+ a5.

Teraz pozostało wykorzystać podaną łączną ilość cukierków.

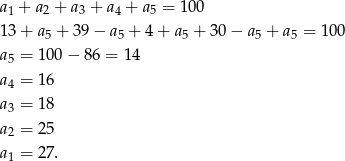
a + a + a + a + a = 100 1 2 3 4 5 13 + a 5 + 39 − a5 + 4 + a5 + 30 − a5 + a5 = 100 a = 100− 86 = 14 5 a4 = 16 a3 = 18 a2 = 25 a1 = 27.

Sposób II

Układ równań można też rozwiązać odrobinę sprytniej (przez 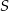S oznaczmy liczbę wszystkich cukierków).

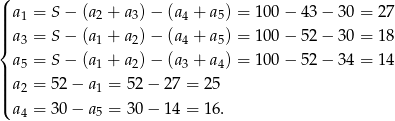
( || a1 = S − (a2 + a3) − (a4 + a5) = 100 − 43 − 30 = 27 ||| |{ a3 = S − (a1 + a2) − (a4 + a5) = 100 − 52 − 30 = 18 a5 = S − (a1 + a2) − (a3 + a4) = 100 − 52 − 34 = 14 ||| a = 52 − a = 5 2− 27 = 25 |||( 2 1 a4 = 30 − a5 = 3 0− 14 = 16.

Sposób III

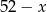Tym razem oznaczmy przez x liczbę cukierków na pierwszym talerzu. Zatem na drugim jest 52 − x cukierków, na trzecim

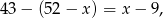
43 − (52 − x) = x − 9 ,

na czwartym

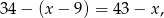
34 − (x − 9) = 43 − x ,

i na piątym

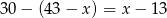
30− (43− x) = x − 13

cukierków. Mamy więc równanie

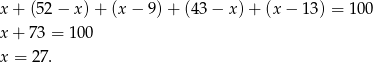
x + (5 2− x)+ (x− 9)+ (4 3− x)+ (x− 13) = 100 x + 7 3 = 100 x = 27.

Stąd łatwo wyliczyć, że na kolejnych talerzach jest 27, 25, 18, 16 i 14 cukierków.  
Odpowiedź: 27, 25, 18, 16, 14 cukierków.

Wersja PDF