/Szkoła średnia/Zadania z treścią

Zadanie nr 1870100

Dodaj do ulubionych
Dodaj do rozwiązanych

Właściciel sklepu muzycznego „Tra-la-la” kupuje w hurtowni płyty zespołu „Emotion” po 30 zł za sztukę i sprzedaje 56 sztuk miesięcznie, po 50 zł za sztukę. Badania rynku wykazały, że każda obniżka ceny płyty o 1 zł, zwiększy liczbę sprzedanych płyt o 4 sztuki (miesięcznie).

  • Wyznacz wzór funkcji miesięcznego zysku właściciela sklepu „Tra-la-la” w zależności od obniżki ceny płyty zespołu „Emotion” (w pełnych złotych). Podaj dziedzinę tej funkcji.
  • Jaką cenę płyty powinien ustalić sprzedawca, aby miesięczny zysk z jej sprzedaży był największy? Oblicz miesięczny największy zysk właściciela sklepu ze sprzedaży płyty „Emotion”.

Rozwiązanie

W chwili obecnej sklep zarabia na płytach

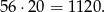
56⋅ 20 = 1120 .
  • Jeżeli cena zostanie obniżona o n złotych to zysk ze sprzedaży będzie wynosił
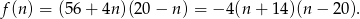
    f(n ) = (56+ 4n)(20 − n ) = − 4(n + 14)(n − 20 ).

    Dziedziną tej funkcji jest zbiór liczb naturalnych nie większych niż 20.

  • Ponieważ wykresem funkcji 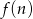f(n ) jest parabola o ramionach skierowanych w dół, wartość największą otrzymamy w wierzchołku paraboli, który jest dokładnie pomiędzy pierwiastkami, czyli w punkcie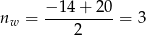
    n = −-14+--20-= 3 w 2

    (oczywiście mogliśmy też wymnożyć nawiasy we wzorze na 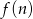f(n) i skorzystać ze wzoru na współrzędne wierzchołka). Zysk dla 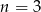n = 3 wynosi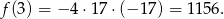

    f (3) = − 4⋅1 7⋅(− 17 ) = 1156.

     
    Odpowiedź: Cena: 47 zł, zysk: 1156 zł.

Wersja PDF