Zadanie nr 1914288

Suma cyfr liczby dwucyfrowej jest mniejsza od 12. Różnica tej liczby i liczby dwucyfrowej otrzymanej po przestawieniu jej cyfr jest równa 36. Wyznacz możliwe wartości liczby .

Rozwiązanie

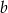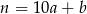Oznaczmy przez cyfrę dziesiątek, a przez cyfrę jedności liczby , tzn. n = 10a + b . Mamy wtedy

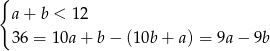
{ a + b < 1 2 36 = 10a+ b− (10b + a) = 9a − 9b

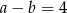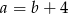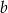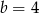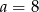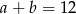Z drugiego równania mamy a− b = 4 , czyli a = b + 4 . Podstawiając teraz za kolejno 0,1,2,3 ( b = 4 jest już za duże, bo wtedy a = 8 i a + b = 12 ) otrzymujemy cztery liczby: 40, 51, 62, 73. Pierwsza z tych liczb nie spełnia jednak założenia podanego w treści zadania, że zmieniając kolejność cyfr liczby również otrzymujemy liczbę dwucyfrową.
Odpowiedź: 51, 62, 73