/Szkoła średnia/Zadania z treścią

Zadanie nr 1944240

Dodaj do ulubionych
Dodaj do rozwiązanych

Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 km/h mniejsza od średniej prędkości, z jaką schodził ze wzgórza.

Rozwiązanie

Sposób I

Powiedzmy, że turysta wchodził pod górę przez 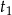t1 godzin, a schodził na dół przez 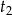t2 godzin. W takim razie

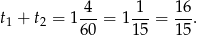
t + t = 1-4- = 1-1- = 1-6. 1 2 6 0 1 5 1 5

Ponadto wiemy, że

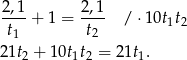
2-,1-+ 1 = 2,1- / ⋅10t1t2 t1 t2 21t2 + 10t1t2 = 21t1.

Podstawiamy teraz w tym równaniu 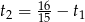t = 16-− t 2 15 1 .

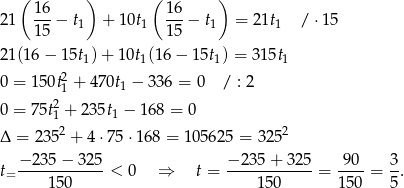
( ) ( ) 16 16 21 ---− t1 + 10t1 ---− t1 = 21t1 / ⋅1 5 15 15 21 (16− 15t1)+ 10t1(16− 15t1) = 315t1 2 0 = 150t1 + 470t1 − 336 = 0 / : 2 0 = 75t21 + 235t1 − 168 = 0 2 2 Δ = 235 + 4 ⋅75 ⋅168 = 105625 = 325 − 235 − 325 − 23 5+ 325 90 3 t= ------------< 0 ⇒ t = ------------ = ----= -. 150 1 50 150 5

W takim razie średnia, z jaką turysta wchodził pod górę była równa

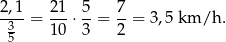
2,1 2 1 5 7 -3--= 1-0 ⋅ 3-= 2-= 3,5 km/h . 5

Sposób II

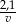Oznaczmy przez v szukaną prędkość z jaką turysta wchodził pod górę. W takim razie czas wejścia pod górę to 2,1 -v- , a czas zejścia to 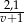2,1 v+1- . Mamy więc równanie

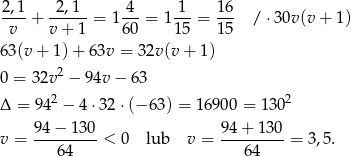
2,1-+ -2,1--= 1 4--= 1 1--= 16- / ⋅3 0v(v + 1) v v+ 1 60 15 15 63(v + 1) + 63v = 32v(v + 1) 2 0 = 32v − 9 4v− 63 Δ = 942 − 4⋅3 2⋅(− 63 ) = 16900 = 1302 94−--130- 94-+-130- v = 64 < 0 lub v = 64 = 3,5.

Zatem 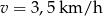v = 3,5 km/h .  
Odpowiedź: 3,5 km/h

Wersja PDF