/Szkoła średnia/Zadania z treścią

Zadanie nr 1988835

Dodaj do ulubionych
Dodaj do rozwiązanych

Wazon ma kształt sześcianu, w którym wydrążony jest walec w taki sposób, że styczne górnej podstawy walca, równoległe do odpowiednich krawędzi górnej podstawy sześcianu, są odległe o 1 cm od tych krawędzi; natomiast odległość między dolną podstawą walca, a dolną podstawą sześcianu (grubość dna) jest równa 2 cm.

PIC

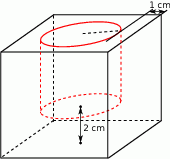
Wiedząc, że stosunek objętości walca do objętości sześcianu jest równy 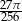272π56 , oblicz

  • długość krawędzi sześcianu;
  • objętość walca;
  • do jakiej wysokości wazonu (licząc od dolnej podstawy walca) będzie sięgać poziom wody, jeśli wlejemy do wazonu 125 ml wody. Wynik podaj z dokładnością do 1 mm.

Rozwiązanie

  • Oznaczmy promień podstawy walca przez r . W takim razie długość krawędzi sześcianu jest równa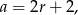
    a = 2r + 2,

    a wysokość walca

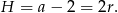
    H = a− 2 = 2r.

    Mamy więc równanie.

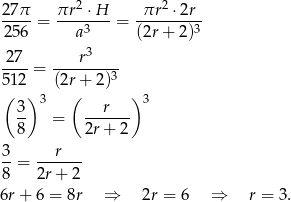
    2 2 27π- = πr--⋅-H-= -πr--⋅2r- 256 a3 (2r + 2)3 2 7 r3 ----= --------3 512 (2r+ 2) ( 3) 3 ( r ) 3 -- = ------- 8 2r + 2 3- --r---- 8 = 2r+ 2 6r+ 6 = 8r ⇒ 2r = 6 ⇒ r = 3.

    Zatem krawędź sześcianu ma długość

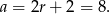
    a = 2r + 2 = 8 .

     
    Odpowiedź: 8 cm

  • Liczymy
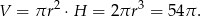
    2 3 V = πr ⋅H = 2πr = 54π .

     
    Odpowiedź: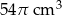 54π cm 3

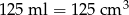  • Jeżeli oznaczmy szukaną wysokość przez x to mamy równanie (125 ml = 1 25 cm 3 )
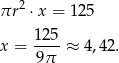
    πr 2 ⋅ x = 125 125 x = ----≈ 4,42. 9π

     
    Odpowiedź: 4,42 cm

Wersja PDF