Zadanie nr 2095000
Z okrągłego skrawka materiału wycięto trójkąt równoboczny jak na rysunku poniżej.
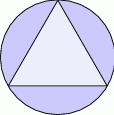
Oblicz jaki procent pola okrągłego skrawka stanowi pole wyciętego trójkąta. Przyjmując, że 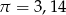 , wynik podaj z dokładnością do 1%.
, wynik podaj z dokładnością do 1%.
Rozwiązanie
Dorysujmy środek koła i promienie łączące go z wierzchołkami trójkąta.
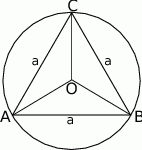
Jeżeli oznaczymy przez  długość boku trójkąta równobocznego, to promień okręgu
długość boku trójkąta równobocznego, to promień okręgu 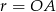 jest równy
jest równy  wysokości trójkąta równobocznego (bo tak środek trójkąta równobocznego dzieli wysokości). Zatem
wysokości trójkąta równobocznego (bo tak środek trójkąta równobocznego dzieli wysokości). Zatem
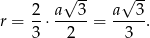
Zatem szukany stosunek pól jest równy (korzystamy ze wzoru na pole trójkąta równobocznego)
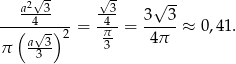
Jeżeli zamienimy to na procenty, to mamy 41%.
Odpowiedź: 41%

