Zadanie nr 2117258
Oblicz ile wynosi suma wszystkich liczb naturalnych 3-cyfrowych.
Rozwiązanie
Wypiszmy te liczby
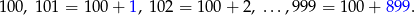
Widać, że jest to suma 900set wyrazów ciągu arytmetycznego.
Mówiąc jeszcze inaczej, liczb od 1 do 999 jest 999. Jak od nich odejmiemy 99 tych, które nie są trzycyfrowe, to zostaje nam 900 liczb.
Zatem
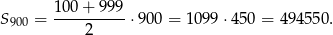
Odpowiedź: 494550

