/Szkoła średnia/Zadania z treścią

Zadanie nr 2379108

Dodaj do ulubionych
Dodaj do rozwiązanych

Droga z miejscowości 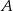A do miejscowości 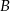B ma długość 26 km. Motocyklista przebył tę drogę w czasie o 1,5 h krótszym niż rowerzysta, który jechał z prędkością o 39 km/h mniejszą. Oblicz, z jaką prędkością jechał motocyklista, a z jaką rowerzysta.

Rozwiązanie

Sposób I

Niech 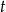t i v oznaczają odpowiednio czas przejazdu oraz prędkość motocyklisty. Z założeń mamy

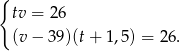
{ tv = 2 6 (v − 39 )(t+ 1,5) = 26.

Podstawiamy 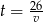t = 26- v z pierwszego równania do drugiego.

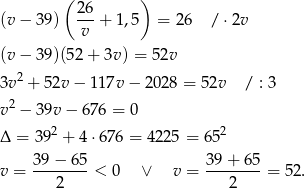
( ) 26- (v − 39) v + 1,5 = 26 / ⋅2v (v − 39)(52 + 3v ) = 52v 3v2 + 52v − 1 17v− 2028 = 52v / : 3 v2 − 39v − 67 6 = 0 2 2 Δ = 39 + 4⋅ 676 = 422 5 = 65 39−--65- 39-+-65- v = 2 < 0 ∨ v = 2 = 52.

Ujemne rozwiązanie odrzucamy i mamy 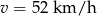v = 52 km/h . Wtedy prędkość rowerzysty to

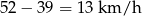
52 − 39 = 13 km/h

Sposób II

Wprowadzamy oznaczenia: 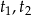t1,t2 niech oznaczają czas przejazdu motocyklisty i rowerzysty, a 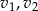v ,v 1 2 niech oznaczają ich prędkości. Z założeń mamy

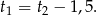
t = t − 1,5. 1 2

Stąd

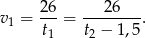
2-6 ---26--- v1 = t = t − 1,5. 1 2

Podstawiamy to do równania

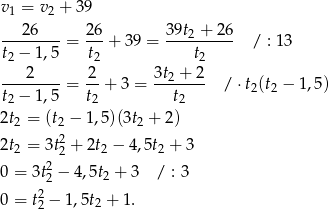
v 1 = v2 + 39 --2-6---= 26-+ 3 9 = 39t2-+-26- / : 13 t2 − 1,5 t2 t2 2 2 3t2 + 2 --------= -- + 3 = ------- / ⋅t2(t2 − 1,5) t2 − 1,5 t2 t2 2t2 = (t2 − 1,5)(3t2 + 2) 2t = 3t2+ 2t − 4,5t + 3 2 2 2 2 0 = 3t22 − 4,5t2 + 3 / : 3 2 0 = t2 − 1 ,5t2 + 1.

Wyznaczamy pierwiastki

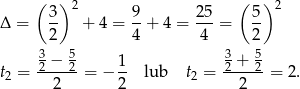
( 3 )2 9 25 ( 5) 2 Δ = -- + 4 = -+ 4 = ---= -- 2 4 4 2 3− 5 1 3 + 5 t2 = 2---2-= − -- lub t2 = 2---2-= 2. 2 2 2

Odrzucamy wynik ujemny i otrzymujemy 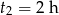t2 = 2 h . Obliczamy prędkość rowerzysty

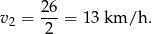
26 v2 = ---= 13 km/h . 2

Teraz pozostało nam tylko obliczyć prędkość motocyklisty

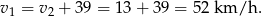
v1 = v 2 + 3 9 = 13 + 39 = 5 2 km/h .

 
Odpowiedź: Prędkość rowerzysty: 13 km/h, motocyklisty: 52 km/h

Wersja PDF