/Szkoła średnia/Zadania z treścią

Zadanie nr 2391387

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz sumę wszystkich liczb dwucyfrowych, które są podzielne przez 4.

Rozwiązanie

Sposób I

Wypiszmy te liczby

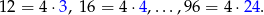
12 = 4 ⋅3, 16 = 4 ⋅4,...,96 = 4 ⋅24 .

Widać, że liczby te tworzą ciąg arytmetyczny o długości 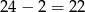24 − 2 = 22 . Jego suma jest równa

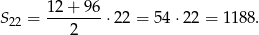
S22 = 12+--96-⋅22 = 54 ⋅22 = 1188. 2

Sposób II

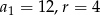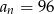Liczby, o których mowa w zadaniu tworzą ciąg arytmetyczny, w którym a1 = 1 2,r = 4 oraz an = 96 . Ze wzoru na n -ty wyraz ciągu arytmetycznego obliczamy n .

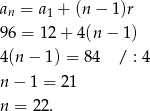
a = a + (n − 1)r n 1 96 = 12 + 4(n − 1 ) 4(n − 1) = 84 / : 4 n− 1 = 21 n = 22.

Pozostało skorzystać ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego.

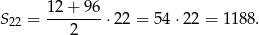
12+ 96 S22 = --------⋅22 = 54 ⋅22 = 1188. 2

 
Odpowiedź: 1188

Wersja PDF