/Szkoła średnia/Zadania z treścią

Zadanie nr 2991934

Dodaj do ulubionych
Dodaj do rozwiązanych

Dziadek założył w banku trzyletnią lokatę pieniężną o stałej rocznej stopie procentowej równej 5% (już po uwzględnieniu podatków i prowizji). Odsetki są kapitalizowane po każdym roku trwania lokaty. Całość środków, otrzymanych z banku po zlikwidowaniu lokaty, dziadek podzielił równo pomiędzy dziewięcioro wnucząt tak, że każde z dzieci otrzymało 1029 zł. Oblicz początkową kwotę lokaty.

Rozwiązanie

Wiemy, że po z likwidowaniu lokaty, dziadek pobrał z banku

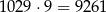
1 029⋅ 9 = 9261

złotych. Załóżmy teraz, że na początku miał x złotych.

Sposób I

Ponieważ dopisanie 5% do kwoty 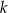k to to samo co

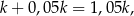
k+ 0,05k = 1,05k ,

czyli pomnożenie 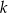k przez 1,05, więc po pierwszym roku miał 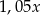1,05x . Po drugim roku miał

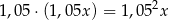
2 1,0 5⋅(1,05x ) = 1,05 x

(dopisujemy odsetki do kwoty z poprzedniego okresu). Po trzecim roku będzie miał

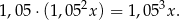
2 3 1,05⋅ (1 ,05 x) = 1,05 x.

Mamy zatem równanie

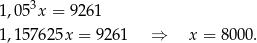
1,053x = 9261 1,157 625x = 9261 ⇒ x = 8000.

Sposób II

Zamiast wyprowadzać wzór na kapitał końcowy (co zrobiliśmy wyżej), możemy od razu z niego skorzystać.

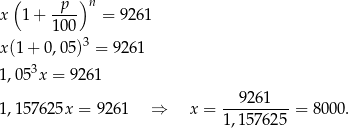
( -p--)n x 1+ 100 = 9 261 3 x(1 + 0,05) = 9 261 1,053x = 9261 1,15762 5x = 926 1 ⇒ x = --9261---= 8000 . 1,157625

 
Odpowiedź: 8000 zł

Wersja PDF