/Szkoła średnia/Zadania z treścią

Zadanie nr 3080559

Dodaj do ulubionych
Dodaj do rozwiązanych

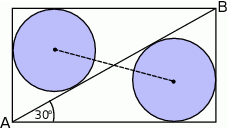
Na rysunku przedstawiony został szkic części parku. Dwie fontanny wpisano w prostokątny klomb kwiatów. Są one styczne do linii przekątnej klombu. Wiedząc, że przekątna klombu ma długość 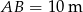AB = 10 m oraz tworzy ona z jednym z boków klombu kąt o mierze 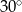30∘ , wyznacz odległość środków tych fontann.

PIC

Rozwiązanie

Długość odcinka 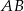AB wyliczymy z trójkąta prostokątnego 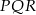PQR , ale najpierw musimy wyliczyć boki długości boków prostokąta oraz promień okręgu wpisanego w trójkąt ABC .

PIC

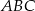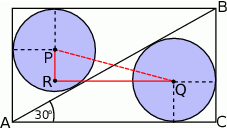
Boki wyliczamy z podanego kąta i długości przeciwprostokątnej 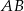AB .

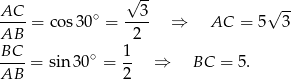
√ -- AC-- ∘ --3- √ -- AB = cos 30 = 2 ⇒ AC = 5 3 BC 1 ----= sin30 ∘ = -- ⇒ BC = 5. AB 2

Promień okręgu wpisanego w trójkąt 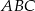ABC wyliczamy ze wzoru na pole 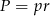P = pr , gdzie 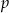p oznacza połowę obwodu trójkąta.

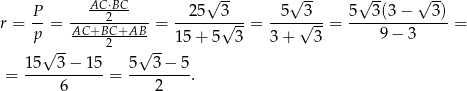
AC-⋅BC- √ -- √ -- √ -- √ -- r = P- = ----2------= --25--3√---= -5--√3--= 5--3(3-−---3)-= p AC+BC-+AB-- 15 + 5 3 3 + 3 9− 3 √ -- 2 √ -- = 1-5--3−--15 = 5--3−--5. 6 2

Możemy teraz obliczyć długości przyprostokątnych trójkąta 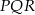P QR .

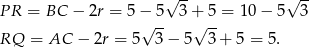
√ -- √ -- PR = BC − 2r = 5 − 5 3 + 5 = 10− 5 3 √ -- √ -- RQ = AC − 2r = 5 3 − 5 3 + 5 = 5.

Zatem szukana odległość jest równa

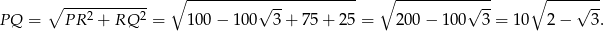
∘ ------------ ∘ ---------√-------------- ∘ ----------√--- ∘ ----√--- PQ = PR 2 + RQ 2 = 100− 100 3 + 75 + 25 = 200 − 10 0 3 = 10 2− 3.

 
Odpowiedź: ∘ ----√--- √ -- √ -- 10 2− 3 m = 5( 6− 2) m

Wersja PDF