/Szkoła średnia/Zadania z treścią

Zadanie nr 3268158

Dodaj do ulubionych
Dodaj do rozwiązanych

Paweł i Gaweł wyruszyli w 500 kilometrową podróż dwoma samochodami. Samochód Pawła poruszał się cały czas ze stałą prędkością, a sposób poruszania się samochodu Gawła przedstawiony jest na poniższym wykresie.

PIC

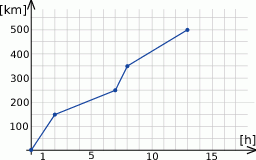
  • Oblicz z jaką prędkością poruszał się samochód Pawła, jeżeli dojechał on do celu 20 minut po Gawle. Wynik podaj w kilometrach na godzinę
  • Przez ile godzin Gaweł jechał wolniej od Pawła?
  • Ile razy, i w której minucie podróży oba samochody się spotkały (nie licząc początku i końca podróży). Wynik podaj z dokładnością do 1 minuty.

Rozwiązanie

  • Z wykresu widzimy, że podróż Gawła trwała
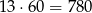
    13 ⋅60 = 780

    minut. Zatem podróż Pawła trwała 800 minut, co daje średnią prędkość

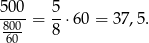
    5-00 = 5⋅6 0 = 37,5. 800 8 60

     
    Odpowiedź: 37,5 km/h

  • Jeżeli oznaczymy kolejne etapy podróży Gawła jak na wykresie,
    PIC

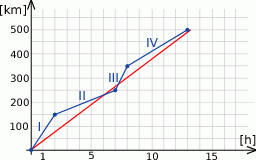
    to mamy średnie prędkości.

    1 50 I : ---- = 75 km/h 2 II : 1-00 = 20 km/h 5 10 0 III : -1-- = 100 km/h IV : 150-= 30 km/h . 5

    Zatem Gaweł jechał wolniej od Pawła w II i IV etapie, czyli w sumie przez

    5 + 5 = 10

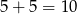
    godzin.  
    Odpowiedź: Przez 10 godzin.

  • W pierwszym etapie podróży Gaweł jechał szybciej od Pawła, więc się nie spotkali. Droga przebyta przez Gawła w II etapie wyraża się wzorem
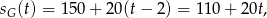
    s (t) = 150+ 20(t− 2) = 110 + 20t, G

    gdzie 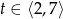t ∈ ⟨2,7 ⟩ . Droga przebyta przez Pawła wyraża się wzorem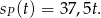

    sP(t) = 37,5t.

    Sprawdźmy czy samochody spotkają się w trakcie II etapu.

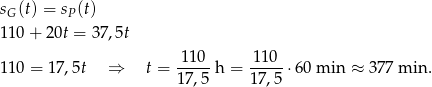
    sG(t) = sP (t) 110 + 20t = 37,5t 110 110 110 = 17,5t ⇒ t = -----h = -----⋅6 0 min ≈ 3 77 min . 17 ,5 17,5

    Podobnie sprawdzamy, czy samochody spotkały się w trakcie III etapu. Prędkość Gawła w tym etapie wyraża się wzorem

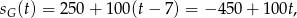
    sG (t) = 2 50+ 100(t− 7) = − 450 + 100t,

    co daje nam równanie

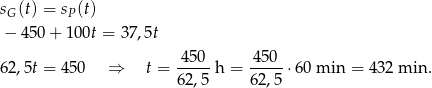
    sG(t) = sP (t) − 450 + 100t = 37,5t 450 450 62,5t = 4 50 ⇒ t = -----h = -----⋅6 0 min = 4 32 min . 62 ,5 62,5

    Wiemy, że do celu Paweł przyjechał po Gawle, więc w IV etapie już go nie dogonił.

    Na koniec drobna uwaga. Jeżeli narysujemy na danym wykresie przebieg podróży Pawła, czyli połączymy początek układu z punktem o współrzędnych 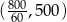800 ( 60 ,500) to punkty przecięcia się tych dwóch wykresów odpowiadają dokładnie znalezionym przez nas spotkaniom obu samochodów.  
    Odpowiedź: Dwa razy, w 377 i 432 minucie.

Wersja PDF