/Szkoła średnia/Zadania z treścią

Zadanie nr 3289503

Dodaj do ulubionych
Dodaj do rozwiązanych

W czasie wycieczki rowerowej uczniowie mieli do przebycia trasę długości 84 km. Podzielili tę trasę na odcinki równej długości i codziennie przejeżdżali wyznaczony odcinek. Gdyby na przebycie całej trasy zużyli o dwa dni więcej, to mogliby dziennie przejeżdżać o 7 km mniej. Ile kilometrów przebywali uczniowie dziennie i ile dni potrzebowali na pokonanie trasy?

Rozwiązanie

Wprowadzamy następujące oznaczenia

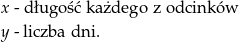
x- długo ść ka żdego z odcink ów y- liczba dni.

Zapisujemy układ równań

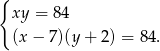
{ xy = 84 (x− 7)(y+ 2) = 84.

Przyrównujemy stronami powyższe równania i rozwiązujemy

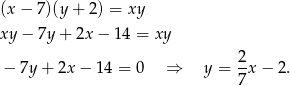
(x − 7)(y + 2) = xy xy − 7y + 2x− 14 = xy 2 − 7y + 2x − 14 = 0 ⇒ y = -x − 2. 7

Podstawiamy do pierwszego równania i rozwiązujemy

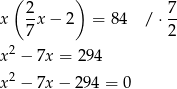
( 2 ) 7 x --x− 2 = 84 / ⋅ -- 7 2 x2 − 7x = 2 94 2 x − 7x − 294 = 0

Obliczamy wyznacznik główny i pierwiastki

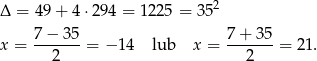
Δ = 49 + 4 ⋅294 = 1 225 = 352 x = 7−--35-= − 1 4 lub x = 7-+-35-= 21. 2 2

Odrzucamy rozwiązanie ujemne i otrzymujemy, że 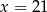x = 21 . Obliczamy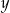 y

y = 2-⋅21 − 2 = 6 − 2 = 4. 7

 
Odpowiedź: Dziennie przejeżdżali 21 km i zajeło im to 4 dni.

Wersja PDF