/Szkoła średnia/Zadania z treścią

Zadanie nr 4024677

Dodaj do ulubionych
Dodaj do rozwiązanych

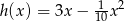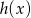Zawodnik kopnął piłkę, która zakreśliła w powietrzu fragment toru opisanego równaniem h (x) = 3x − 110x 2 (x oznacza poziomą odległość piłki od zawodnika, a h (x) wysokość na jakiej znajduje się piłka). Oblicz, na jaką największą wysokość wzniosła się piłka.

Rozwiązanie

Wykresem funkcji 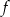f jest parabola zwrócona ramionami w dół. Zatem największą wartość przyjmuje w wierzchołku.

PIC

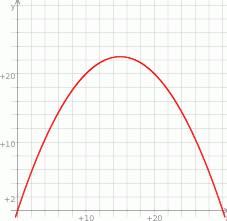
Przekształćmy wzór funkcji 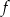f

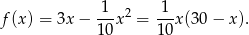
f(x ) = 3x − -1-x2 = -1-x(30 − x). 10 10

Widać, że pierwiastkami są liczby 0 i 30. Wierzchołek paraboli znajduje się dokładnie w środku pomiędzy pierwiastkami, więc

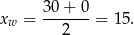
xw = 30+--0-= 1 5. 2

Teraz już łatwo policzyć największą wysokość

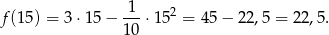
1 f(15) = 3 ⋅15 − ---⋅1 52 = 45 − 22,5 = 2 2,5. 10

 
Odpowiedź: 22,5

Wersja PDF