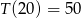/Szkoła średnia/Zadania z treścią

Zadanie nr 4085528

Dodaj do ulubionych
Dodaj do rozwiązanych

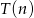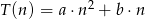Doświadczalnie ustalono, że czas T(n ) , liczony w sekundach, potrzebny na alfabetyczne ułożenie n kartek z nazwiskami wyraża się, z dobrym przybliżeniem, wzorem T(n ) = a⋅ n2 + b⋅n . Ułożenie 10 kartek trwa średnio 20 sekund, a 30 kartek średnio 90 sekund. Wyznacz wzór funkcji 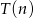T(n ) i oblicz, ile kartek można ułożyć średnio w ciągu 50 sekund.

Rozwiązanie

Mamy układ równań

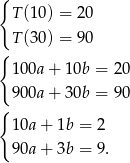
{ T(10 ) = 20 T(30 ) = 90 { 100a + 10b = 20 900a + 30b = 90 { 10a + 1b = 2 90a + 3b = 9 .

Odejmujemy od drugiego równania pierwsze pomnożone przez 3 (żeby skrócić b ).

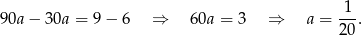
1-- 90a − 3 0a = 9 − 6 ⇒ 60a = 3 ⇒ a = 20.

Z pierwszego równania mamy wtedy

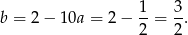
b = 2 − 10a = 2 − 1-= 3. 2 2

Pozostało rozwiązać równanie 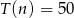T (n) = 50 .

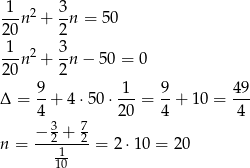
1 3 ---n2 + -n = 50 20 2 -1-n2 + 3n − 50 = 0 20 2 9 1 9 49 Δ = 4-+ 4 ⋅50⋅ 20-= 4-+ 10 = 4-- 3 7 n = −-2 +-2-= 2 ⋅10 = 2 0 -1 10

(od razu wybraliśmy dodatni pierwiastek).  
Odpowiedź: 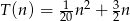-1 2 3 T (n) = 20n + 2n , T (20) = 50

Wersja PDF