/Szkoła średnia/Zadania z treścią

Zadanie nr 4174752

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczbę 7 dzielimy na trzy części tak aby pierwsza była dwa razy większa od drugiej. Jak należy dokonać podziału, aby suma kwadratów wszystkich trzech części była najmniejsza?

Rozwiązanie

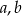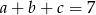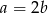Szukamy trzech liczb dodatnich a,b i c takich, że a + b+ c = 7 , a = 2b oraz wyrażenie 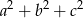a2 + b2 + c2 ma być możliwie największe. Korzystając z podanych warunków, wyrażenie to przyjmuje postać

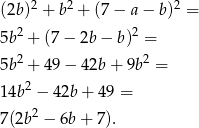
(2b )2 + b2 + (7 − a − b)2 = 2 2 5b + (7 − 2b − b) = 5b 2 + 49 − 4 2b+ 9b2 = 2 14b − 4 2b+ 49 = 7(2b 2 − 6b + 7).

Szukamy teraz najmniejszej wartości funkcji

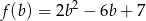
2 f(b) = 2b − 6b+ 7

na przedziale 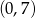(0,7) . Sprawdzamy gdzie jest wierzchołek paraboli będącej wykresem tej funkcji.

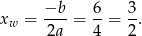
xw = −b--= 6-= 3. 2a 4 2

Ponieważ punkt ten jest w przedziale 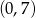(0,7) , jest to szukana wartość 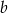b . Daje ona 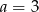a = 3 i c = 52 .  
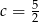Odpowiedź: Szukany rozkład: 7 = 3+ 3+ 5 2 2

Wersja PDF