/Szkoła średnia/Zadania z treścią

Zadanie nr 4254395

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.

Rozwiązanie

Mamy układ

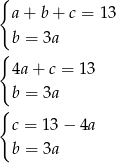
{ a+ b+ c = 13 b = 3a { 4a+ c = 13 b = 3a { c = 13 − 4a b = 3a

i chcemy znaleźć rozwiązanie z minimalnym 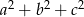a2 + b2 + c2 . Z układu mamy

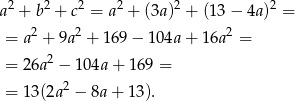
a2 + b2 + c2 = a2 + (3a )2 + (1 3− 4a )2 = 2 2 2 = a + 9a + 169 − 104a + 16a = = 26a2 − 104a + 1 69 = = 13(2a2 − 8a + 13 ).

Aby znaleźć wartość najmniejszą tego wyrażenia, szukamy wartości najmniejszej funkcji 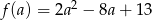f(a) = 2a 2 − 8a + 13 . W tym miejscu jest jednak pewien delikatny szczegół. Ponieważ liczby mają być dodatnie, a nie może być zupełnie dowolne. Dokładniej:

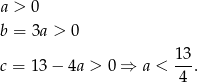
a > 0 b = 3a > 0 1 3 c = 13− 4a > 0 ⇒ a < ---. 4

Szukamy zatem minimum funkcji 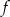f na przedziale 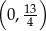( ) 0, 13 4 . Liczymy pierwszą współrzędną wierzchołka paraboli będącej wykresem tej funkcji:

xw = 2.

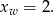
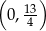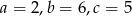Ponieważ punkt ten leży w przedziale ( ) 0, 134 , to właśnie w nim funkcja osiąga minimum. Otrzymujemy stąd a = 2,b = 6,c = 5 .  
Odpowiedź: a = 2 ,b = 6,c = 5

Wersja PDF