/Szkoła średnia/Zadania z treścią

Zadanie nr 5180058

Dodaj do ulubionych
Dodaj do rozwiązanych
  • Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
  • Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.

Rozwiązanie

  • Jeżeli oznaczymy szukane liczby przez 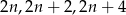2n ,2n + 2,2n + 4 to mamy równanie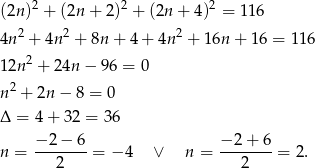
    (2n)2 + (2n + 2 )2 + (2n + 4)2 = 116 2 2 2 4n + 4n + 8n + 4+ 4n + 16n + 16 = 116 2 12n + 24n − 96 = 0 n2 + 2n − 8 = 0 Δ = 4+ 32 = 36 −-2−--6 −-2+--6 n = 2 = − 4 ∨ n = 2 = 2 .

    Skoro liczby mają być ujemne to 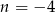n = −4 i szukane liczby to -8,-6,-4.  
    Odpowiedź: -8,-6,-4

  • Przy oznaczeniach z poprzedniego podpunktu, mamy
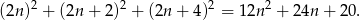
    (2n)2 + (2n + 2)2 + (2n + 4 )2 = 12n2 + 24n + 2 0.

    Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, więc wartość najmniejszą otrzymamy w wierzchołku, czyli dla

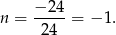
    − 24 n = -----= − 1. 24

    Daje to nam liczby -2,0,2.  
    Odpowiedź: -2,0,2

Wersja PDF