/Szkoła średnia/Zadania z treścią

Zadanie nr 5248379

Dodaj do ulubionych
Dodaj do rozwiązanych

Do zbiornika o pojemności 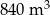3 840 m można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 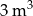3 m 3 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 32 godziny krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.

Rozwiązanie

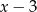Powiedzmy, że pierwsza rura dostarcza do zbiornika x metrów sześciennych wody na godzinę. Wtedy druga rura dostarcza x − 3 metrów sześciennych na godzinę. Możemy teraz napisać równanie wiążące czasy napełniania zbiornika przez obie rury.

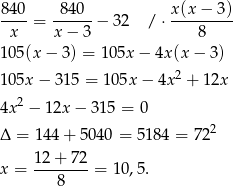
840- -840-- x-(x−--3) x = x − 3 − 3 2 / ⋅ 8 105(x − 3 ) = 105x − 4x (x− 3) 105x − 3 15 = 105x − 4x2 + 12x 2 4x − 12x − 3 15 = 0 2 Δ = 144 + 5040 = 5184 = 7 2 12+--72- x = 8 = 1 0,5.

W takim razie obie rury w ciągu godziny dostarczają

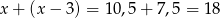
x + (x − 3) = 10 ,5 + 7 ,5 = 18

metrów sześciennych wody i cały zbiornik będzie napełniony w

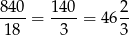
840- 14-0 2- 18 = 3 = 46 3

godziny.  
Odpowiedź: 46 godzin i 40 minut

Wersja PDF