/Szkoła średnia/Zadania z treścią

Zadanie nr 5471671

Dodaj do ulubionych
Dodaj do rozwiązanych

Asia wrzucała do skarbonki monety dwu i pięciozłotowe. Po przeliczeniu zawartości skarbonki okazało się, że w skarbonce znajdowało się 395 monet, a uzbierana kwota wynosi 1195 złotych. Oblicz ile monet każdego rodzaju było w skarbonce.

Rozwiązanie

Sposób I

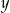Jeżeli oznaczymy przez x i y liczby monet dwu i pięciozłotowych to mamy układ równań

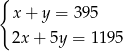
{ x + y = 395 2x + 5y = 1195

Odejmując od drugiego równania dwa razy pierwsze (żeby skrócić x ) mamy

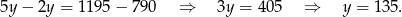
5y − 2y = 119 5− 7 90 ⇒ 3y = 405 ⇒ y = 135.

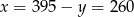Zatem x = 3 95− y = 260 .

Sposób II

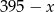Mogliśmy też od razu ułożyć równanie z jedną niewiadomą. Jeżeli x oznacza liczbę dwuzłotówek, to 5 złotówek jest 395 − x i mamy równanie

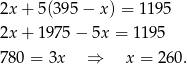
2x + 5 (3 95− x) = 119 5 2x + 1 975− 5x = 11 95 780 = 3x ⇒ x = 260.

Zatem pięciozłotówek jest 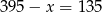395 − x = 1 35 .  
Odpowiedź: 260 po 2 zł i 135 po 5 zł

Wersja PDF