Zadanie nr 5593499

Na podstawie zasad dynamiki można udowodnić, że torem ruchu rzuconej piłki – przy pominięciu oporów powietrza – jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości 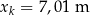, licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie 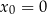, 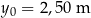. Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:

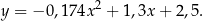
Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.

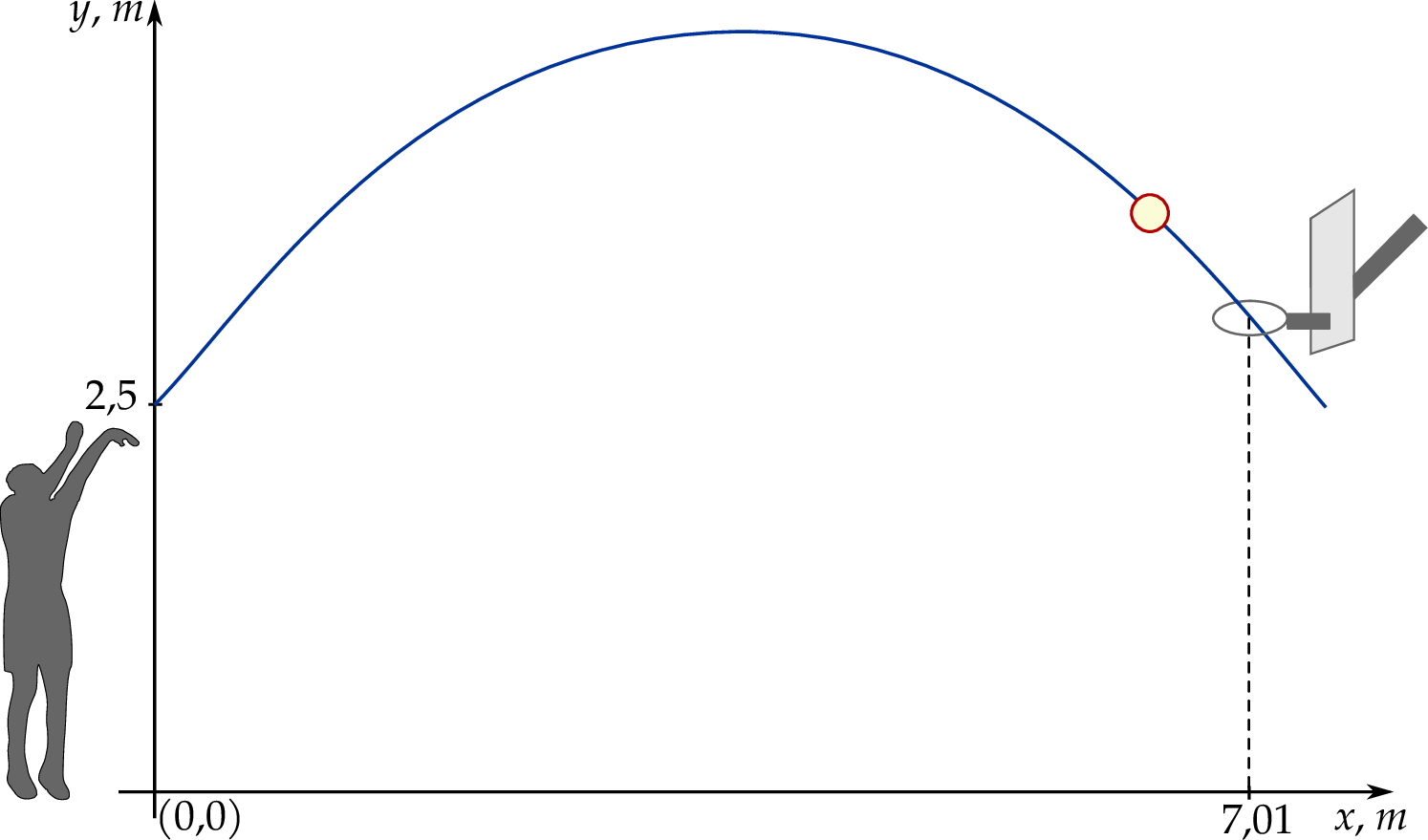
W opisanym rzucie piłka przeleciała swobodnie przez obręcz kosza i upadła na parkiet. Przyjmij, że obręcz kosza nie miała siatki, a na drodze rzutu nie było żadnej przeszkody. Promień piłki jest równy 0,12 m. Oblicz współrzędną środka piłki w momencie, w którym piłka dotknęła parkietu. Wynik zapisz w metrach w zaokrągleniu do drugiego miejsca po przecinku.