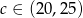Zadanie nr 6074821

Oto dwie funkcje określające miesięczne zapotrzebowanie rynku (popyt) na szynkę (w tonach) oraz wielkość miesięcznych dostaw (podaż) szynki na rynek (w tonach).

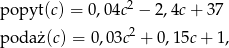
popyt (c) = 0,04c 2 − 2,4c + 37 2 poda ż(c) = 0 ,03c + 0,15c+ 1,

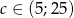gdzie –cena szynki w zł za kg i c ∈ (5 ;25) . Oblicz przy jakiej cenie szynki

podaż będzie równoważyć popyt (tzw. cena równowagi);
nadwyżka podaży nad popytem będzie przekraczać 11 ton miesięcznie.

Rozwiązanie

Musimy rozwiązać równanie
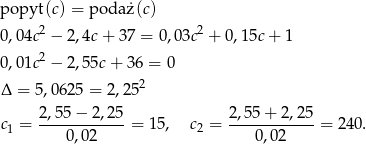
$popyt (c) = poda ż(c) 2 2 0 ,04c − 2,4c+ 37 = 0,03c + 0,15c + 1 0 ,01c2 − 2,55c+ 36 = 0 2 Δ = 5,0 625 = 2,25 2,55 − 2,25 2,55+ 2,25 c1 = ------------= 15, c2 = ------------= 240. 0 ,02 0,02$

Ze względu na podany w treści zadania przedział zmienności , mamy .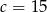
Odpowiedź: 15zł
Musimy rozwiązać nierówność
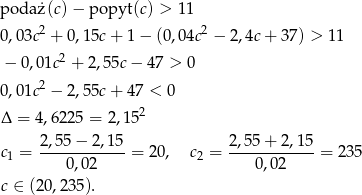
$poda ż(c)− popyt (c) > 11 0,03c2 + 0,15c + 1 − (0,04c2 − 2,4c + 37) > 11 2 − 0,01c + 2,55c− 47 > 0 0,01c2 − 2,55c + 47 < 0 Δ = 4,6225 = 2 ,1 52 2,55 − 2,1 5 2,55 + 2,15 c1 = ------------ = 20, c2 = ------------= 235 0,02 0,02 c ∈ (20,235).$

Uwzględniając podany w treści zadania przedział zmienności , mamy .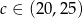
Odpowiedź: