/Szkoła średnia/Zadania z treścią

Zadanie nr 6450785

Dodaj do ulubionych
Dodaj do rozwiązanych

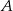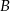Dwaj rowerzyści wyjechali naprzeciw siebie z dwóch miejscowości A i B położonych od siebie w odległości 180 km. Rowerzysta jadący z miejscowości 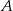A wyjechał o godzinę później od drugiego i jechał ze średnią prędkością 3 km/h mniejszą niż rowerzysta jadący z miejscowości 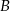B . Stosunek średnich prędkości rowerzystów wyrażał się liczbą z przedziału 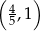(4 ) 5 ,1 . Rowerzyści spotkali się w odległości 72 km od miejscowości 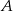A . Z jakimi średnimi prędkościami jechali obaj rowerzyści?

Rozwiązanie

Oznaczmy przez 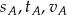sA,tA ,vA , odpowiednio: drogę, czas podróży oraz średnią prędkość (do momentu spotkania) rowerzysty, który wyjechał z miejscowości 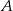A . Analogicznie definiujemy liczby 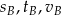sB ,tB ,vB , dla rowerzysty, który wyjechał z miejscowości B .

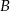Z założeń mamy

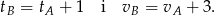
tB = tA + 1 i vB = vA + 3.

Rowerzyści spotkali się w odległości 72 km od miejscowości 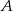A , więc

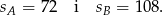
sA = 72 i sB = 108 .

Liczymy

v = v + 3 B A sB-= sA-+ 3 tB tA 108 7 2+ 3tA -------= --------- tA + 1 tA 1 08tA = (tA + 1)(7 2+ 3tA ) 2 1 08tA = 72tA + 3tA + 72 + 3tA / − 108tA 0 = 3t2A − 33tA + 72 / : 3 2 0 = tA − 11tA + 24.

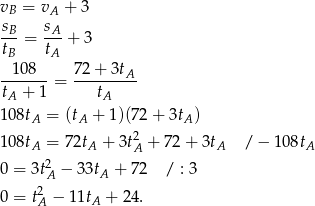
Liczymy wyróżnik i pierwiastki

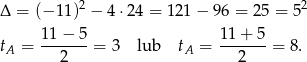
2 2 Δ = (− 11) − 4⋅24 = 121 − 96 = 2 5 = 5 11− 5 11 + 5 tA = --2----= 3 lub tA = --2----= 8.

Stąd

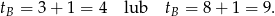
t = 3 + 1 = 4 lub t = 8+ 1 = 9. B B

Teraz już łatwo obliczyć średnie prędkości

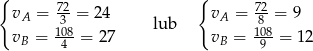
{ { v = 72 = 2 4 v = 72 = 9 A 1308 lub A 1808 vB = -4-= 27 vB = -9- = 12

Liczymy stosunek średnich prędkości

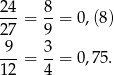
24-= 8-= 0,(8) 27 9 9 3 12-= 4-= 0,75.

Tylko pierwsza z tych liczb należy do przedziału 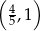( ) 4,1 5 . Zatem

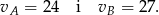
v = 24 i v = 27. A B

 
Odpowiedź: 24 km/h i 27 km/h

Wersja PDF