Zadanie nr 6469272
Z miejscowości 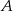 i
i 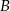 oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości
oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości 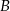 do miejscowości
do miejscowości 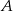 jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości
jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości 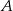 do miejscowości
do miejscowości 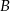 wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości
wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości 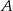 przebył do tego miejsca
przebył do tego miejsca 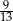 całej drogi z
całej drogi z 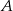 do
do 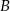 . Z jakimi średnimi prędkościami jechali obaj rowerzyści?
. Z jakimi średnimi prędkościami jechali obaj rowerzyści?
Rozwiązanie
Punkt spotkania rowerzystów jest oddalony od miejscowości 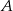 o
o
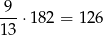
kilometrów. Jeżeli oznaczymy średnią prędkość pierwszego rowerzysty (jadącego z 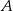 do
do 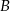 ) przez
) przez  , a czas (w godzinach), po jakim spotkał on się z drugim rowerzystą przez
, a czas (w godzinach), po jakim spotkał on się z drugim rowerzystą przez 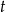 , to z podanych informacji mamy układ równań
, to z podanych informacji mamy układ równań
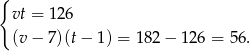
Przekształćmy drugie równanie
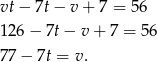
Podstawiamy otrzymane wyrażenie do równości 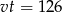 .
.
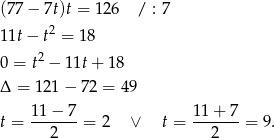
Pierwsze rozwiązanie daje nam 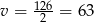 , czyli prędkość drugiego rowerzysty byłaby większa od 25 km/h, co jest sprzeczne z treścią zadania. Zatem
, czyli prędkość drugiego rowerzysty byłaby większa od 25 km/h, co jest sprzeczne z treścią zadania. Zatem 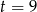 i
i 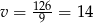 . Drugi rowerzysta jechał ze średnią prędkością
. Drugi rowerzysta jechał ze średnią prędkością 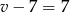 .
.
Odpowiedź: 14 i 7 km/h

