/Szkoła średnia/Zadania z treścią

Zadanie nr 6477483

Dodaj do ulubionych
Dodaj do rozwiązanych

Pewna firma komputerowa produkuje dwa typy komputerów. Koszt części potrzebnych do złożenia komputera I rodzaju wynosi 1500 zł, a II rodzaju 2000 zł. Firma zyskuje na każdym sprzedanym komputerze I typu 400 zł, a II typu 600 zł. Tygodniowo firma przeznacza na potrzebne materiały co najwyżej 32500 zł i sprzedaje 20 komputerów. Ile komputerów każdego rodzaju powinna firma produkować tygodniowo, aby zysk jej był jak największy? Jaki to będzie zysk?

Rozwiązanie

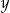Powiedzmy, że firma produkuje tygodniowo x komputerów I rodzaju i y komputerów II rodzaju. Oczywiście zysk będzie tym większy, im więcej jest produkowanych komputerów, więc od razu możemy założyć, że 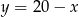y = 20− x . Informacja o kosztach produkcji daje nierówność

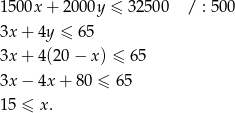
1500x + 2 000y ≤ 32 500 / : 500 3x + 4y ≤ 6 5 3x + 4(20 − x) ≤ 65 3x − 4x + 80 ≤ 65 15 ≤ x.

Zatem maksymalna liczba komputerów II rodzaju to 5. Sprawdźmy jeszcze jak zachowuje się funkcja zysku.

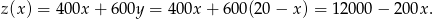
z (x) = 400x + 6 00y = 40 0x+ 600(20 − x ) = 12000 − 200x .

stąd widać wyraźnie, że im mniej komputerów I rodzaju tym lepiej. Zatem optymalne proporcje produkcji to 15 komputerów I rodzaju i 5 drugiego rodzaju. Zysk wynosi wtedy

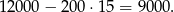
12000 − 2 00⋅1 5 = 9000.

 
Odpowiedź: 15 I rodzaju i 5 II rodzaju. Zysk: 9000 zł

Wersja PDF