/Szkoła średnia/Zadania z treścią

Zadanie nr 6704955

Dodaj do ulubionych
Dodaj do rozwiązanych

Metalowy stożek, którego tworząca o długości 10 jest nachylona do płaszczyzny podstawy pod kątem 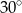30 ∘ , przetopiono na sześć jednakowych kulek. Oblicz promień kulki.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

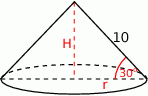
Liczymy

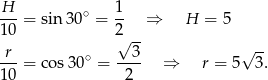
H--= sin 30∘ = 1- ⇒ H = 5 10 2√ -- r ∘ 3 √ -- ---= co s30 = ---- ⇒ r = 5 3. 10 2

Zatem stożka objętość jest równa

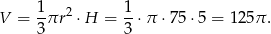
1- 2 1- V = 3πr ⋅H = 3 ⋅π ⋅75⋅ 5 = 125π .

Stożek został przetopiony na sześć kulek, więc jedna kulka ma objętość 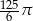125π 6 . Jeżeli oznaczymy przez 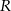R przez promień kulki, to mamy równanie

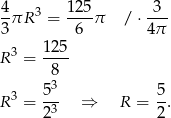
4- 3 1-25 -3- 3 πR = 6 π / ⋅4 π 12 5 R 3 = ---- 8 3 53- 5- R = 23 ⇒ R = 2.

 
Odpowiedź: 5 2

Wersja PDF