/Szkoła średnia/Zadania z treścią

Zadanie nr 6762050

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma cyfr liczby trzycyfrowej wynosi 8, zaś suma kwadratów jej cyfr jest równa 30. Jeśli w liczbie zamienimy cyfry skrajne to otrzymana liczba będzie o 396 większa od początkowej. Znajdź tę liczbę.

Rozwiązanie

Jeżeli szukana liczba to 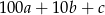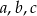10 0a+ 10b+ c (a,b,c to odpowiednio cyfry setek, dziesiątek i jedności) to mamy warunki

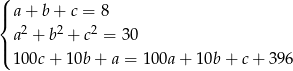
( |{ a+ b+ c = 8 a2 + b2 + c2 = 30 |( 100c + 10b + a = 1 00a+ 10b + c+ 396

Z ostatniego równania mamy

99c = 9 9a+ 396 ⇒ c = a + 4.

Wstawiamy to do dwóch pierwszych równań.

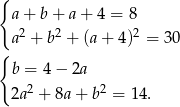
{ a + b + a + 4 = 8 a2 + b2 + (a + 4)2 = 30 { b = 4− 2a 2 2 2a + 8a + b = 14.

Podstawiamy 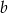b z pierwszego równania do drugiego.

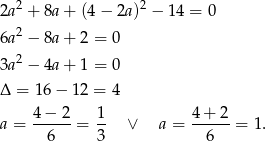
2 2 2a + 8a+ (4− 2a) − 14 = 0 6a2 − 8a+ 2 = 0 2 3a − 4a+ 1 = 0 Δ = 16− 12 = 4 a = 4-−-2-= 1- ∨ a = 4-+-2-= 1 . 6 3 6

Zatem 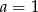a = 1 . Stąd 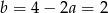b = 4 − 2a = 2 i c = a+ 4 = 5 .  
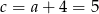Odpowiedź: 125

Wersja PDF