/Szkoła średnia/Zadania z treścią

Zadanie nr 7018430

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprzedawca zegarków kupił w hurtowni za 5746 złotych dwa rodzaje zegarków: damskie i męskie, przy czym kupił trzy razy więcej zegarków damskich niż męskich. Przy ponownym zakupie takiej samej ilości zegarków, otrzymał 10% rabatu na cenę zakupu zegarka damskiego oraz 10 zł upustu na cenę zakupu zegarka męskiego. Dzięki otrzymanym rabatom, łączny koszt zakupu zmalał do 5265 zł. Wiedząc, że po udzieleniu rabatu, cena męskiego zegarka była dwa razy wyższa od ceny zegarka damskiego, oblicz pierwotne ceny zegarków.

Rozwiązanie

Oznaczmy przez x liczbę zakupionych zegarków męskich, a przez c cenę po rabacie jednego zegarka damskiego. W takim razie zegarków damskich było 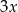3x , a jeden zegarek męski po rabacie kosztował 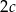2c . Ceny przed rabatem wynosiły odpowiednio 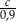c-- 0,9 i 2c+ 10 .

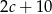Z podanych informacji o kosztach zakupu mamy układ równań

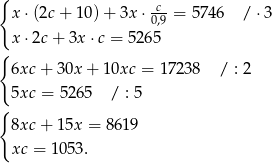
{ -c- x ⋅(2c+ 10)+ 3x ⋅0,9 = 5746 / ⋅ 3 x ⋅2c+ 3x ⋅c = 5265 { 6xc + 30x + 10xc = 17 238 / : 2 5xc = 5265 / : 5 { 8xc + 15x = 8619 xc = 1 053.

Podstawiając 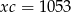xc = 105 3 do pierwszego równania otrzymujemy

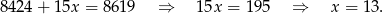
8424 + 15x = 8619 ⇒ 15x = 19 5 ⇒ x = 13 .

Zatem

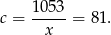
c = 1053-= 81. x

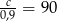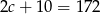i oryginalne ceny zegarków były równe c-- 0,9 = 90 oraz 2c + 10 = 172 .  
Odpowiedź: Damski: 90 zł, męski: 172 zł.

Wersja PDF