/Szkoła średnia/Zadania z treścią

Zadanie nr 7220542

Dodaj do ulubionych
Dodaj do rozwiązanych

Pewien kierowca, jadąc z miasta 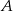A do miasta 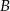B , zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta 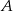A , jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?

Rozwiązanie

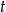Jeżeli przez v oznaczymy średnią prędkość samochodu a przez t czas w którym przejechał 117 km, to wiemy, że

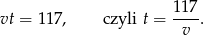
vt = 117 , czyli t = 117. v

Wiemy ponadto, że jeżeli średnia prędkość będzie większa o 12 km/h, to czas przejazdu będzie krótszy o 0,2 h. Otrzymujemy stąd równanie:

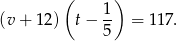
( ) (v+ 12) t− 1- = 117 . 5

Po podstawieniu za 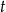t z poprzedniej równości dostajemy:

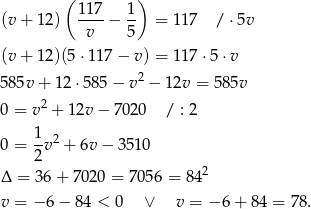
( ) (v+ 12) 11-7− 1- = 11 7 / ⋅5v v 5 (v+ 12)(5 ⋅117 − v) = 11 7⋅5 ⋅v 585v + 12 ⋅585 − v2 − 12v = 585v 2 0 = v + 12v − 70 20 / : 2 1 2 0 = --v + 6v− 3510 2 2 Δ = 36+ 7020 = 70 56 = 84 v = − 6 − 84 < 0 ∨ v = − 6 + 84 = 78 .

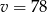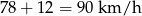Oczywiście pierwsze rozwiązanie odrzucamy i mamy v = 78 . W takim razie w drodze powrotnej samochód poruszał się ze średnią prędkością 78 + 12 = 90 km/h .  
Odpowiedź: 90 km/h

Wersja PDF