/Szkoła średnia/Zadania z treścią

Zadanie nr 7420004

Dodaj do ulubionych
Dodaj do rozwiązanych

Janek i Ludwik mają razem 54 lata. Trzynaście lat temu Ludwik był 3 razy starszy od Janka. Ile lat temu Ludwik był dwa razy starszy od Janka?

Rozwiązanie

Sposób I

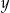Jeżeli oznaczymy przez x i y wiek odpowiednio Janka i Ludwika, to mamy układ równań

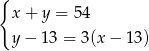
{ x + y = 54 y − 1 3 = 3(x − 13)

Odejmujemy od pierwszego równania drugie (żeby skrócić 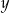y ).

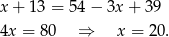
x + 1 3 = 54 − 3x + 39 4x = 80 ⇒ x = 20.

Zatem 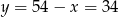y = 54 − x = 34 .

Różnica wieku między Ludwikiem i Jankiem jest równa 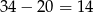3 4− 20 = 14 , więc Ludwik był dwa razy starszy od Janka, gdy Janek miał 14 lat, czyli 6 lat temu.

Sposób II

Skoro teraz mają łącznie 54 lata, to 13 lat temu mieli łącznie 28 lat. W dodatku Ludwik był 3 razy starszy od Janka, czyli

x + 3x = 2 8 ⇒ x = 7 ,

gdzie przez x oznaczyliśmy wiek Janka 13 lat temu. Zatem teraz Janek ma 20 lat, a Ludwik 34.

Różnica wieku między Ludwikiem i Jankiem jest równa 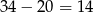3 4− 20 = 14 , więc Ludwik był dwa razy starszy od Janka, gdy Janek miał 14 lat, czyli 6 lat temu.  
Odpowiedź: 6 lat temu.

Wersja PDF