Zadanie nr 7503454
Za wynajęcie autobusu na wycieczkę uczniowie klasy IA mieli zapłacić 1800 złotych. Ponieważ 4 uczniów zrezygnowało z tej wycieczki, każdy z pozostałych uczniów zapłacił o 15 zł więcej. Oblicz, ilu uczniów jest w klasie IA.
Rozwiązanie
Sposób I
Jeżeli oznaczymy liczbę uczniów przez  , a oryginalny koszt uczestnictwa jednej osoby w wycieczce przez
, a oryginalny koszt uczestnictwa jednej osoby w wycieczce przez  to mamy układ równań
to mamy układ równań
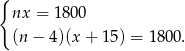
Przekształćmy drugie równanie
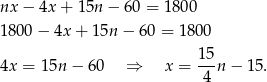
Podstawiamy to wyrażenie do równości 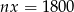 i mamy
i mamy
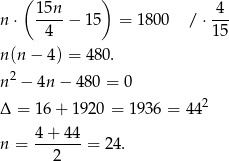
Sposób II
Jeżeli oznaczmy liczbę uczniów w klasie przez  to wiemy, że początkowo każdy z nich miał zapłacić
to wiemy, że początkowo każdy z nich miał zapłacić 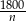 . Po rezygnacji 4 uczniów koszt ten wzrósł do
. Po rezygnacji 4 uczniów koszt ten wzrósł do 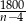 . Z drugiej strony wiemy, że wysokość składki wzrosła o 15 zł. Mamy więc równanie
. Z drugiej strony wiemy, że wysokość składki wzrosła o 15 zł. Mamy więc równanie
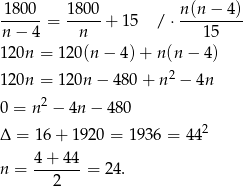
Odpowiedź: 24 osoby

