/Szkoła średnia/Zadania z treścią

Zadanie nr 7555217

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 24 minut.

Rozwiązanie

Sposób I

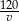Oznaczmy szukaną prędkość średnią przez v . Zatem czas przejazdu (w godzinach) wynosi 12v0 i mamy równanie

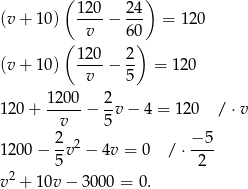
( ) (v + 10) 120-− 24- = 120 v 60 ( 120 2 ) (v + 10) ----− -- = 120 v 5 1-200 2- 120 + v − 5 v− 4 = 120 / ⋅v 2 − 5 1200 − -v2 − 4v = 0 / ⋅---- 5 2 v2 + 10v − 30 00 = 0.

Rozwiązujemy to równanie kwadratowe.

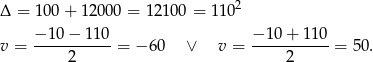
Δ = 10 0+ 1 2000 = 12 100 = 11 02 − 10 − 110 − 10+ 110 v = -----------= − 60 ∨ v = -----------= 50. 2 2

Ujemne rozwiązanie odrzucamy i mamy 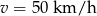v = 50 km/h .

Sposób II

Oznaczmy czas w jakim autobus przejechał 120 km przez 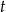t . W takim razie średnia prędkość autobusu to 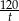120 t i z podanych informacji mamy równanie

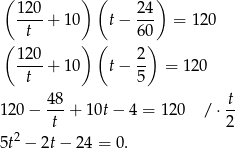
( 120 ) ( 24) ----+ 10 t− --- = 120 ( t ) ( 60) 120 2 -t--+ 10 t− 5- = 120 120 − 48-+ 10t− 4 = 120 / ⋅ t- t 2 5t2 − 2t − 24 = 0.

Rozwiązujemy to równanie kwadratowe.

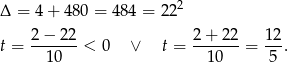
Δ = 4 + 480 = 484 = 22 2 2−-2-2- 2+--22- 12- t = 10 < 0 ∨ t = 10 = 5 .

Ujemne rozwiązanie odrzucamy i mamy 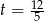t = 152 . Stąd

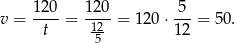
v = 1-20 = 1-20 = 12 0⋅ 5--= 50 . t 12 12 5

 
Odpowiedź: 50 km/h

Wersja PDF