Zadanie nr 7682954
Sprzedawca kupuje miesięcznie w hurtowni laptopy, płacąc 1200 zł za sztukę. W chwili obecnej sprzedaje 20 laptopów miesięcznie w cenie 1400 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 10 zł zwiększa o 2 liczbę sprzedanych laptopów. Jaką powinien ustalić cenę laptopa, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?
Rozwiązanie
Powiedzmy, że sprzedawca obniży cenę o 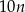 złotych. Wtedy sprzeda
złotych. Wtedy sprzeda 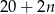 laptopów i na każdym zarobi
laptopów i na każdym zarobi 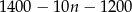 . W takim razie zysk sprzedawcy wyraża się wzorem
. W takim razie zysk sprzedawcy wyraża się wzorem
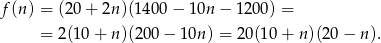
Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość osiąga w wierzchołku, czyli dokładnie pomiędzy pierwiastkami. Maksymalny zysk otrzymamy zatem dla
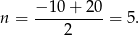
Zysk dla tej wartości  jest równy
jest równy
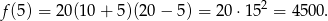
Nowa cena laptopa to 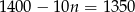 .
.
Odpowiedź: Cena: 1350 zł, zysk: 4500 zł

