Zadanie nr 7811037
Dwa motocykle wyjechały z miast 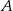 i
i 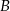 oddalonych od siebie o 360 km. Motocykl jadący z miasta
oddalonych od siebie o 360 km. Motocykl jadący z miasta 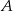 do miasta
do miasta 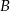 wyjechał o 30 minut wcześniej niż motocykl jadący z miasta
wyjechał o 30 minut wcześniej niż motocykl jadący z miasta 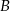 do miasta
do miasta 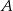 i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.
i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.
Rozwiązanie
Sposób I
Oznaczmy prędkość pierwszego motocykla przez  . Oznaczmy ponadto przez
. Oznaczmy ponadto przez 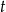 czas w jakim przejechał on połowę drogi, czyli 180 km. Mamy zatem
czas w jakim przejechał on połowę drogi, czyli 180 km. Mamy zatem
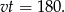
Teraz pozostało zapisać informację o drugim motocyklu. Wiemy, że jechał on z prędkością 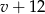 oraz połowę drogi przejechał w czasie
oraz połowę drogi przejechał w czasie 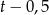 (bo wyjechał 30 minut później). Zatem
(bo wyjechał 30 minut później). Zatem
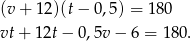
Ponieważ 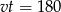 mamy stąd
mamy stąd

Podstawiamy to wyrażenie w równości 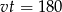 .
.
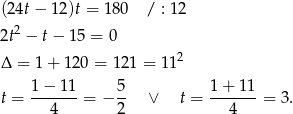
Stąd 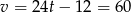 . Zatem drugi motocykl jechał z prędkością
. Zatem drugi motocykl jechał z prędkością 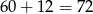 .
.
Sposób II
Jeżeli przez  oznaczymy prędkość pierwszego motocykla, to połowę drogi przebył on w czasie
oznaczymy prędkość pierwszego motocykla, to połowę drogi przebył on w czasie 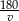 . Drugi motocykl dotarł do połowy drogi w czasie
. Drugi motocykl dotarł do połowy drogi w czasie 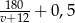 . Mamy więc równanie
. Mamy więc równanie
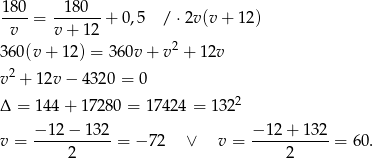
Zatem prędkość drugiego motocykla jest równa 72 km/h.
Odpowiedź: 60 km/h oraz 72 km/h

