Zadanie nr 8089783
Dwa pociągi: towarowy o długości 490 m i osobowy o długości 210 m, jadą naprzeciw siebie po dwóch równoległych torach i spotykają się w miejscu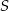 
. Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce 
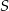jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
Rozwiązanie
Oznaczmy prędkość pierwszego pociągu przez 
, prędkość drugiego przez 
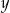. Mijając się, każdy z pociągów pokonuje dystans (względem drugiego pociągu) równy sumie ich długości, czyli 
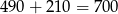metrów. Rzeczywiście, wygodnie jest myśleć o początku jednego z pociągów – najpierw musi dojechać do końca drugiego pociągu, a potem musi jeszcze przejechać dystans równy swojej własnej długości, żeby jego koniec dojechał do końca drugiego pociągu. Ponadto, pociągi mijając się jadą ze względną prędkością 
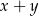, co daje nam równanie
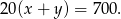
Inny sposób myślenia prowadzący do tego samego równania może być następujący: w momencie spotkania końce pociągów są od siebie odległe o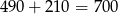 
metrów, a mijanie zakończy się, gdy się pokryją. Ponieważ zbliżają się do siebie z prędkością 
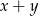, otrzymujemy powyższe równanie.
Czas przejazdu pierwszego pociągu przez punkt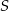 
to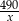 
, a czas przejazdu drugiego pociągu to 
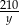. Daje to nam drugie równanie
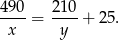
Mamy więc układ równań
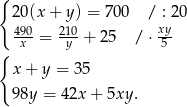
Podstawiamy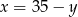 
z pierwszego równania do drugiego i mamy
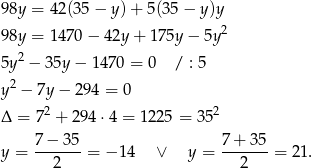
Ujemne rozwiązania odrzucamy i mamy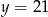 
. Zatem 
.
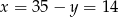Odpowiedź: 
