Zadanie nr 8093436
Fragment palisady wokół średniowiecznego grodu składa się z coraz krótszych pionowych bali. Najwyższy z bali ma długość 350 cm, a każdy kolejny jest krótszy o 5 cm. Wiedząc, że całkowita długość wszystkich bali wynosi 50 m oblicz ile jest tych bali i jaka jest długość najkrótszego z nich.
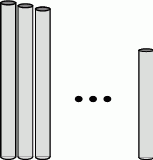
Rozwiązanie
Długości bali tworzą ciąg arytmetyczny o pierwszym wyrazie 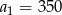 i różnicy
i różnicy 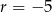 . Jeżeli jest
. Jeżeli jest  bali, to ze wzoru na sumę
bali, to ze wzoru na sumę  początkowych wyrazów ciągu arytmetycznego mamy
początkowych wyrazów ciągu arytmetycznego mamy
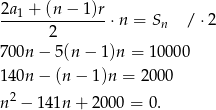
Dalej
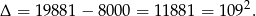
Stąd 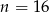 lub
lub 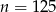 . Drugą z tych wartości odrzucamy, bo wszystkich bali jest co najwyżej
. Drugą z tych wartości odrzucamy, bo wszystkich bali jest co najwyżej 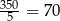 . Pozostało wyliczyć długość ostatniego bala.
. Pozostało wyliczyć długość ostatniego bala.
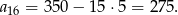
Jeżeli ktoś jest ciekawy dlaczego z równania kwadratowego wyszły nam dwie możliwe wartości  , to wynika to z faktu, że od pewnego momentu wyrazy malejącego ciągu
, to wynika to z faktu, że od pewnego momentu wyrazy malejącego ciągu 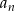 robią się ujemne i suma zaczyna się zmniejszać. Jak wyliczyliśmy, dla
robią się ujemne i suma zaczyna się zmniejszać. Jak wyliczyliśmy, dla 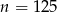 będzie ona znowu równa 5000. Ujemne wyrazy ciągu są jednak wykluczone przez treść zadania.
będzie ona znowu równa 5000. Ujemne wyrazy ciągu są jednak wykluczone przez treść zadania.
Odpowiedź: Ilość: 16. Długość najkrótszego: 275 cm

