/Szkoła średnia/Zadania z treścią

Zadanie nr 8589086

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie liczby trzycyfrowe, w których cyfra setek jest o 3 większa od cyfry dziesiątek i 2 razy większa od cyfry jedności.

Rozwiązanie

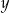Oznaczmy prze x cyfrę setek, y cyfrę dziesiątek i przez z cyfrę jedności. Wówczas z założeń mamy

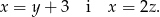
x = y + 3 i x = 2z.

Porównując x -y z tych równań mamy

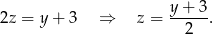
2z = y+ 3 ⇒ z = y+--3. 2

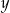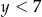Musimy również pamiętać, że te niewiadome mają reprezentować cyfry, więc wszystkie muszą być liczbami naturalnymi mniejszymi niż 10. Dodatkowo y musi być liczbą nieparzystą (żeby z był całkowity) i y < 7 (żeby było 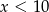x < 10 ). W takim razie możliwe wartości 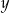y to: 1, 3, 5. Mamy wtedy odpowiednio:

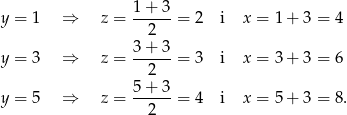
1 + 3 y = 1 ⇒ z = ------= 2 i x = 1+ 3 = 4 2 y = 3 ⇒ z = 3-+-3-= 3 i x = 3+ 3 = 6 2 5-+-3- y = 5 ⇒ z = 2 = 4 i x = 5+ 3 = 8.

Zatem wszystkie liczby spełniające warunki zadania to: 412, 633, 854.  
Odpowiedź: 412 ,633,854

Wersja PDF